Замена двух плоскостей проекций

Часто при определении действительной величины какой-либо гео­метрической фигуры или для получения более полного (наглядного) ее изображения замены одной плоскости проекций бывает недостаточ­но. В таких случаях приходится осуществлять замену двух плоскос­тей проекций.

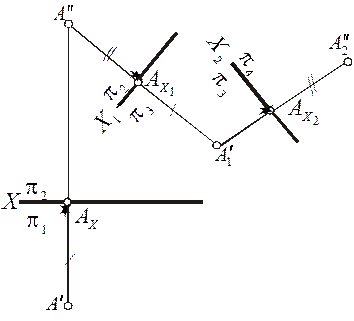
Рис. 15

.

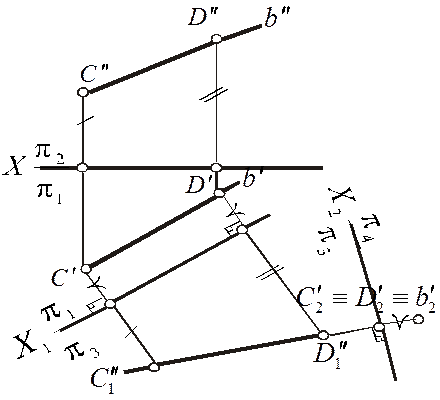
Рис. 16

Рассмотрим, как определяются новые ортогональные проекции

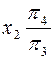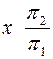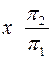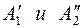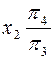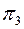точки в новой системе плоскостей проекции , если известны ее про­екции в старой системе плоскостей . Пусть А' и А" — проекции точки А на исходных плоскостях проекций (рис. 15).Для того чтобы определить положение новых проекций в системе , заменяем вначале плоскость новой плоскостью . Точку, через которую проводится новая ось, и направление оси можно выбирать произвольно. Следует следить лишь за тем, чтобы не происходило накла­дывания новых проекций на старые и чтобы геометрические фигуры, расположенные в первой четверти пространства, оставались в нем и после замены плоскости проекции.

Новая горизонтальная проекция 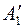точки А будет принадлежать од­ной линии связи, проходящей через старую фронтальную проекцию 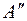и перпендикулярную к новой оси х₁, и будет удалена от новой оси на такое же расстояние, на какое старая горизонтальная проекция точ­ки была удалена от старой оси х. Поэтому для определения положе­ния проекции 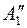достаточно от точки 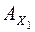на продолжении перпенди­куляра 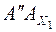отложить, 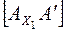равный отрезку .

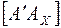Положение новой фронтальной проекции точки в системе плоскостей проекции 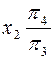определяется аналогично только что рассмотрен­ному случаю с той лишь разницей, что теперь за исходную (старую) систему будем принимать систему 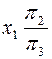и от нее переходить к системе 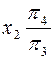. В этом случае плоскость 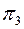не меняет своего положения в

пространстве, следовательно, не изменится положение и горизонталь­ной проекции 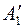. Фронтальная проекция 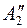будет определена, если из 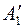восставить перпендикуляр к оси х₂ и отложить на нем от точки 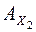отрезок 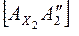, равный расстоянию от точки 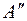до оси х₁- .

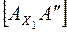Зная правила построения проекций одной точки в новой системе плоскостей проекций, можно построить новые проекции любого чис­ла точек, а следовательно, и любой геометрической фигуры.

На рис. 16 показан пример перевода отрезка [CD] прямой общего положения b в положение 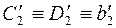отрезка фронтально проецирующей прямой b . Вначале заменой плоскости 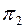плоскостью 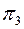пере­водим отрезок [CD] в положение 7 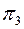-задача 1, затем, заменив плоскостью 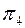, ставим отрезок по отношению к плоскости 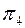в проецирующее положение-задача 2.

Метод замены плоскости проекций может применяться при решении многих задач, рассмотрим только некоторые из них.

ПРИМЕР 1. Определить расстояние от точки К до плоскости, заданной 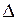ABC (рис. 17).

РЕШЕНИЕ.

1. Переводим плоскость 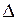ABC в проецирующее положение. Для этого переходим от системы 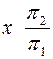к 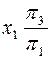; направление новой оси х₁, выбирается перпенди­кулярным к горизонтальной проекции горизонтали плоскости треугольника.

2. Проецируем 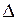АВС на новую плос­кость 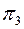(плоскость 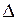ABC спроецируется на 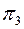в ).

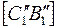Проецируем на ту же плоскость точку .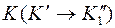

Через точку 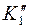проводим 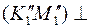отрезку 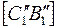. Искомое расстояние .

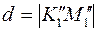Решение задачи упрощается, если плос­кость задана следами, так как отпадает необходимость в проведении проекций линий уровня.Решение задачи упрощается, если плос­кость задана следами, так как отпадает необходимость в проведении проекций линий уровня.

ПРИМЕР 2. Определить расстояние от точки К до плоскости a, заданной следа­ми (рис. 18) .

РЕШЕНИЕ. Заменяем плоскость плоскостью 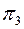, для этого проводим новую ось 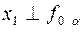. На 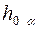отмечаем произвольную точку 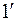и определяем ее новую горизонтальную проекцию на плоскости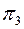 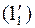. Через точк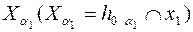и и 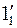проводим 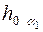.Определяем новую горизонтальную проекцию точки 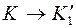. Из точки 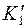опускаем перпендикуляр на 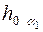и отмечаем точку его пересечения с 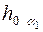- 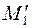. Длина отрезка 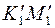укажет искомое расстояние.

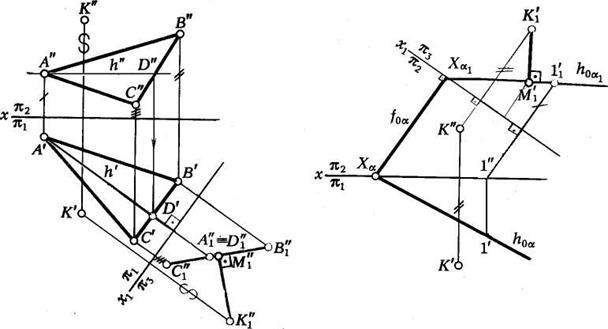
Рис. 17 Рис. 18