Виды параллельных проекций

Классификация параллельных проекций показана на рис. 18.

Рис. 18. Виды параллельных проекций.

В ортографических и аксонометрических проекциях проецирующие лучи перпендикулярны картинной плоскости (направление проецирования совпадает с нормалью к проекционной плоскости).

Во всех параллельных проекциях грани отображаемого объекта, параллельные картинной плоскости, изображаются без искажения формы и размеров; параллельные в пространстве прямые сохраняют параллельность и после проецирования, а также остаются постоянными относительные длины параллельных в исходном пространстве линий.

Самой простой из параллельных проекций является ортографическая проекция, при которой картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис. 19), а проецирующие лучи параллельны одной из координатных осей.

Рис. 19. Ортографическая проекция на плоскость z = 0.

Матрица проецирования на координатную плоскость z = 0 имеет вид:

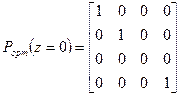, (x.1)

Аналогично, матрицы проецирования на плоскости x = p и y = q равны:

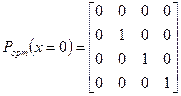, (x.2)

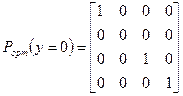. (x.3)

Наиболее часто используются наборы ортографических проекций отдельных сторон объекта (вид спереди, вид сверху, вид сбоку).

В аксонометрических проекциях нормаль к картинной плоскости (а, следовательно, и направление проецирования) не совпадает ни с одной из координатных осей (рис.20).

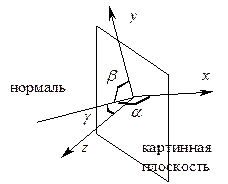
Рис. 20. Аксонометрическая проекция.

В зависимости от взаимного расположения картинной плоскости и осей координат выделяют следующие виды аксонометрических проекций:

а) триметрия – нормаль к картинной плоскости образует с координатными осями попарно различные углы (a ¹ b, b ¹ g, a ¹ g);

б) диметрия – два угла между нормалью к картинной плоскости и координатными осями равны;

в) изометрия – все три угла между нормалью к картинной плоскости и координатными осями равны (a = b = g).

Каждая из этих проекций получается комбинацией поворотов с последующим параллельным проецированием.

При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия). На рис.21 приведена (аксонометрическая прямоугольная) изометрическая проекция куба со стороной A. При этой проекции плоскость проецирования наклонена ко всем главным координатным осям под одинаковым углом. Стандартом регламентируется коэффициент сжатия, равный 0.82, а также расположение и взаимные углы главных координатных осей, равные 120^° как это показано в левом верхнем углу рис.21. Обычно сжатие не делается.

Рис.21: Аксонометрическая прямоугольная изометрическая проекция куба со стороной A

При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы. Триметрическая проекция строится последовательными поворотами вокруг координатных осей, совершаемыми в произвольном порядке, с последующим проецированием на плоскость z = 0. Коэффициенты искажения (отношение длины проекции отрезка к его истинной длине) по каждой из проецируемых координатных осей не равны друг другу.

Диметрия – это частный случай триметрической проекции с двумя одинаковыми коэффициентами искажения (третий коэффициент может иметь любое значение). Диметрическая проекция может быть получена путем поворота на угол j вокруг оси ординат, затем поворота на угол y вокруг оси абсцисс и проецирования вдоль оси аппликат:

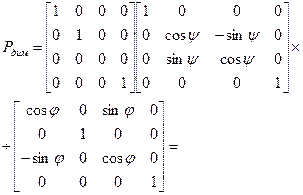
. (x.4)

Найдем величины этих углов поворота.

Квадраты длин проекций единичных векторов координатных осей, совпадающие с коэффициентами искажения по этим осям, равны:

f_x² = cos²j + sin²j sin²y,

f_y² = cos²y,

f_z² = sin²j + cos²j sin²y. (x.5)

Приравнивая любые два коэффициента искажения получают ограничения, налагаемые в случае диметрии на значения углов j и y.

Если f_х² = f_y², то:

),

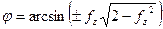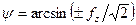. (x.6)

В изометрической проекции все три коэффициента искажения равны:

f_х² = f_y² = f_z². (x.7)

Для изометрии получаем:

sin²j = ½, j =± 45⁰, sin²y = 1/3, y = ± 35,26⁰.

При косоугольных проекциях проецирующие прямые не перпендикулярны картинной плоскости, картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей. Таким образом, косоугольные проекции сочетают в себе свойства ортографических и аксонометрических проекций.

Косоугольная проекция на плоскость z = 0 задается значениями двух углов: a и b, где a – это угол между осью абсцисс и проекцией оси аппликат на картинную плоскость, а b – это угол наклона проецирующих прямых к картинной плоскости (рис. 6.4).

Рассмотрим косоугольную проекцию точки N(0, 0, 1) на плоскость z=0. В результате проецирования точка N преобразуется в точку N*(a, b). Коэффициент искажения f по оси аппликат равен длине проекции единичного вектора (0 0 1):

f = ctgb.

Косоугольная проекция любой точки получается путем сдвига на величину za вдоль оси x, на величину zb вдоль оси y и последующего проецирования на плоскость z=0. Матрица косоугольной проекции:

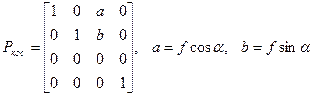, (x.8)

Наиболее часто используют две косоугольных проекции – кавалье и кабине.

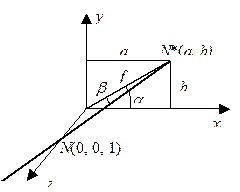
Рис. 22. Косоугольная проекция точки N(0, 0, 1) на плоскость z =0.

Проекция кавалье получается, когда угол между картинной плоскостью и проецирующими прямыми b=45⁰. В этой проекции коэффициенты искажения для каждой из проецируемых координатных осей одинаковы и равны единице (т.е. без искажения):

f=1, a=cosa, b=sina.

Результат проекции кавалье выглядит неестественно утолщенным (см рис 23).

Рисунок 23.. Проекция Кавалье куба со стороной А.

Рис. 24: Аксонометрическая косоугольная фронтальная диметрическая проекция куба со стороной A

У проекции кабине (см рис. 24)коэффициент искажения для ребер, перпендикулярных картинной плоскости, составляет ½:

f=1/2, a=0,5cosa, b=0,5sina.

Для получения проекции кабине угол b между картинной плоскостью и проецирующими прямыми должен составлять 63.43⁰.

Угол a может быть любым, однако, наиболее часто используются проекции со значениями угла a=30⁰ или a=45⁰.