Центральные (перспективные) проекции

В центральных проекциях грани отображаемого объекта, параллельные картинной плоскости, изображаются без искажения формы, но с искажением размера.

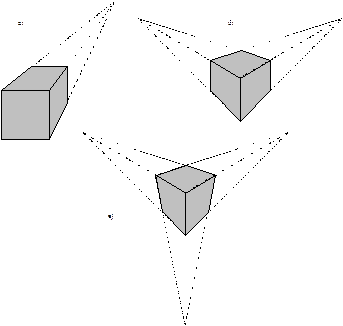
Рисунок 24 Центральные проекции куба: а) одноточечная, б) двухточечная, в) трехточечная.

Центральные проекции любой совокупности параллельных прямых, которые не параллельны картинной плоскости, будут сходиться в точке схода. Точка схода прямых, параллельных одной из координатных осей, называется главной точкой схода. Т.к. координатных осей три, то и главных точек схода не может быть больше трех.

В зависимости от расположения осей координат и картинной плоскости различают одно-, двух- и трехточечные центральные проекции.

Одноточечная проекция получается, когда картинная плоскость совпадает с одной из координатных плоскостей (или параллельна ей). Т.е., только одна ось координат не параллельна картинной плоскости и имеет главную точку схода.

Двухточечная проекция получается, когда только одна из координатных осей параллельна картинной плоскости. Две другие оси координат не параллельны картинной плоскости и имеют две главные точки схода. При изображении объектов, расположенных на поверхности земли, наиболее часто используется двухточечная проекция, при которой картинной плоскости параллельна вертикальная ось координат. Обе главные точки схода расположены на одной горизонтальной линии – линии горизонта (рис. 6.5). При трехточечной проекции все три координатные оси не параллельны картинной плоскости и, следовательно, имеются три главные точки схода.

Рассмотрим более подробно случай одноточечного проецирования точки Р на плоскость z=0 с центром проецирования С, лежащим на оси z (рис.25 ).

Точка A проецируется на экран как A¢. Расстояние от наблюдателя до проекционной плоскости равно k. Необходимо определить координаты точки A¢ на экране. Обозначим их x_э и y_э. Из подобия треугольников A_yA_zN и y_эON находим, что

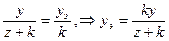(x.9)

аналогично для x:

. (x.10)

Рис. 25. Вывод формул центральной проекции.

Рис. 26. Другой способ вычисления координат точек в центральной перспективной проекции.

Напомним, что k -это расстояние, а наблюдатель находится в точке N = (0,0,-k). Если точку наблюдения поместить в начало координат, а проекционную плоскость на расстояние a, как показано на рисунке 26, то формулы для x_э и y_э примут вид:

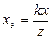, (x.11)

Формулы (x.10) более удобны при необходимости простым образом приближать или удалять наблюдателя от проекционной плоскости. Формулы (x.11) требуют меньше времени для вычислений за счет отсутствия операции сложения.

Рассмотрим точку трехмерного пространства (a,b,c). Если представить эту точку как однородное представление точки двумерного пространства, то ее координаты будут (a/c,b/c). Сравнивая эти координаты со вторым видом формул, выведенных для центральной перспективной проекции, легко заметить, что двумерное представление точки с координатами (a,b,c) выглядит как ее проекция на плоскость z = 1, как показано на рис. 27.

Рис. 27. Проекция точки (a,b,c) на плоскость z = 1.

Аналогично, рассматривая применение однородных координат для векторов трехмерного пространства, можно представить трехмерное пространство как проекцию четырехмерного пространства на гиперплоскость w = 1, если (x,y,z)®(wx,wy,wz,w) = (x,y,z,1). .

В однородных координатах преобразование центральной перспективы можно определить матричной операцией. Эта матрица записывается в виде:

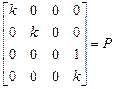
Покажем, что эта матрица определяет преобразование точки объекта, заданной в однородных координатах, в точку перспективной проекции (также в однородных координатах). Пусть p = (x,y,z) – точка в трехмерном пространстве. Ее однородное представление v = (wx,wy,wz,w). Умножим v на P:

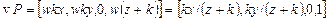
это в точности повторяет формулы (x.10), выведенные для центральной перспективы.

Из-за особенностей человеческого зрения к удаленным от наблюдателя объектам лучше применять перспективную проекцию, к достаточно близким (на расстоянии вытянутой руки) – ортографическую или аксонометрическую, а к еще более близким объектам – обратную перспективную проекцию.

Для создания стереоизображений используются две центральные проекции, центры которых совпадают с расположением глаз гипотетического наблюдателя, т.е. они расположены на некотором расстоянии друг от друга на прямой, параллельной картинной плоскости. После выполнения проецирования получают два изображения объекта – для левого и правого глаза. Устройство вывода должно обеспечивать подачу этих изображений к каждому глазу пользователя отдельно. Для этого может использоваться система цветных или поляризационных фильтров. Более сложные устройства вывода (например, шлемы) подают каждое из изображений на отдельные экраны для каждого глаза.

Все рассмотренные выше проекции относятся к классу плоских геометрических проекций, т.к. проецирование производится на плоскость (а не искривленную поверхность) и с помощью пучка прямых линий (а не кривых). Этот класс проекций наиболее часто используются в компьютерной графике. В отличие от нее, в картографии часто используются неплоские или негеометрические проекции.