Параметрические бикубические поверхности

Параметрические бикубические поверхности задаются многочленами третьей степени от двух параметров s и t. Как и прежде, будем рассматривать только уравнение для координаты х:

x(s, t) = a_11xs³t³ + a_12xs³t² + a_13xs³t + a_14xs³ +

+ a_21xs²t³ + a_22xs²t² + a_23xs²t + a_24xs² +

+ a_31xst³ + a_32xst² + a_33xst + a_34xs +

+ a_41xt³ + a_42xt² + a_43xt + a_44x. (4.20)

Или:

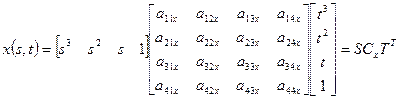. (4.21)

где: S = [s³ s² s 1], и T = [t³ t² t 1].

Матрица С_x задает коэффициенты бикубического многочлена. Существуют еще матрицы С_y и С_z, которые определяют коэффициенты бикубических уравнений y(s, t) и z(s, t).

Изменяя оба параметра s и t от 0 до 1, можно определить все точки на куске поверхности. Если одному из параметров присвоить постоянное значение, а второй параметр изменять в пределах 0…1, то в результате получается кубическая кривая.

Форма Эрмита для задания бикубической поверхности: перепишем уравнение кубической кривой Эрмита от параметра s так, чтобы геометрический вектор Эрмита был не константой, а функцией от параметра t:

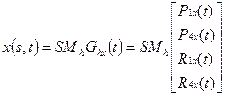. 4.22

При фиксированном значении параметра t функции P_1x(t) и P_4x(t) описывают х-компоненты начальной и конечной точек кривой, задаваемой параметром s. Аналогично, R_1x(t) и R_4x(t) описывают касательные векторы в конечных точках кубической кривой. Каждая из кривых P_1x(t), P_4x(t), R_1x(t), R_4x(t) представлена кубическим многочленом в форме Эрмита:

, ,

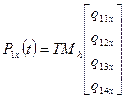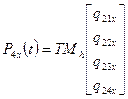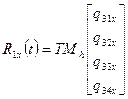, (4.23)

Объединяя эти четыре выражения в одно с учетом известного матричного выражения 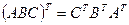, получим:

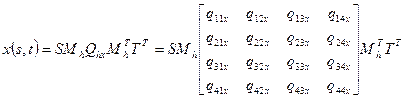(4.25)

Таким образом, бикубическая поверхность Эрмита задается 16 параметрами(см. рис.), из которых:

q_11x = x(0, 0) = P₀₀,

q_12x = x(0, 1) = P₀₁,

q_21x = x(1, 0) = P₁₀,

q_22x = x(1, 1) = P₁₁

– координаты углов куска поверхности;

q_13x = dx/dt (0, 0) = dP₀₀/dt, q_14x = dx/dt (0, 1) = dP₀₁/dt,

q_23x = dx/dt (1, 0) = dP₁₀/dt, q_24x = dx/dt (1, 1) = dP₁₁/dt,

q_31x = dx/ds (0, 0) = dP₀₀/ds, q_32x = dx/ds (0, 1) = dP₀₁/ds,

q_41x = dx/ds (1, 0) = dP₁₀/ds, q_42x = dx/ds (1, 1) = dP₁₁/ds

– х-компоненты касательных векторов в угловых точках для каждой из ограничивающих кусок поверхности параметрических кривых;

q_33x = d²x/dsdt (0, 0) = dP²₀₀/dsdt, q_34x = d²x/dsdt (0, 1) = dP²₀₁/dsdt,

q_43x = d²x/dsdt (1, 0) = dP²₁₀/dsdt, q_44x = d²x/dsdt (1, 1) = dP²₁₁/dsdt

– частные производные по обоим параметрам s и t в угловых точках куска поверхности (кривизна).

Рис. Параметры для поверхности Эрмита

При соединении кусков бикубических поверхностей должны выполняться условия непрерывности: кривые, заданные на общем ребре, должны быть одинаковыми (должны совпадать начальные и конечные точки кривых и значения касательных векторов к кривым в этих точках); касательные вектора, пересекающие ребро, должны иметь одно и тоже направление для обоих сочленяющихся кусков.

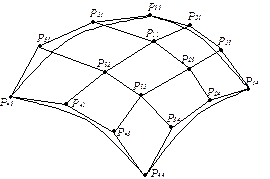
Рис. Управляющие точки поверхности Безье

Уравнения для кусков Безье выводятся также, как и для формы Эрмита. В результате получается:

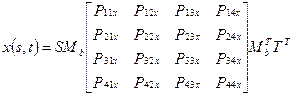. (4.30)

Геометрическая матрица Р_bx состоит из 16 управляющих точек, причем точки Р_11х, Р_14х, Р_41х и Р_44х являются угловыми точками куска поверхности (см.рис)

Поверхности Безье, также как и кривые, обладают свойством выпуклых оболочек.

При соединении двух кусков поверхностей для выполнения условия непрерывности необходимо равенство четырех управляющих точек, принадлежащих общим ребрам кусков. Кроме того, для достижения непрерывности касательного вектора требуется, чтобы две четверки управляющих точек, лежащих по обеим сторонам общего ребра были коллинеарны (лежали на одной прямой) четверке управляющих точек общего ребра и друг другу. Отношения длин коллинеарных отрезков должны быть постоянными.

Куски в форме В-сплайнов представляются в виде:

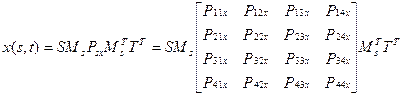(4.31)

Шестнадцать управляющих точек задают кусок поверхности, находящийся около четырех центральных точек Р₂₂, Р₂₃, Р₃₂ и Р₃₃.