Шаг 4. Поворот вокруг оси z.

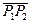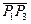На рис. 16 показаны и после шага 3, когда Р₂'' лежит на отрицательной полуоси z, а Р₃''' - в точке

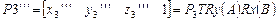
Поворот производится на положительный угол С, для которого

cosC = y₃'''/D₂, sinC = x₃'''/D₂, D₂ = .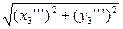

После шага 4 получается конечный результат.

Результирующая матрица

T(-x1,-y1,-z1)×Ry(A)×Rx(B)×Rz(C) = T×R

описывает искомое преобразование.

Рис. 16. Поворот вокруг оси z; проекция 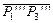поворачивается до совмещения с осью у

Для построения матрицы поворотов можно воспользоваться другим, более простым в вычислительном плане способом, основанным на свойстве ортогональности матриц поворотов.

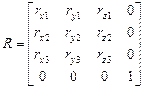
Верхняя подматрица размером 3´3 ортогональная матрица, составленная из трех векторов R_x = [r_x1 r_x2 r_x3], R_y = [r_y1 r_y2 r_y3] и R_z = [r_z1 r_z2 r_z3], в которые будут преобразованы орты осей x, y и z соответственно.

Единичный вектор, который должен лечь вдоль оси Z

.

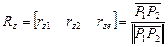Здесь 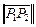- длина вектора .

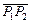Вектор, перпендикулярный плоскости, построенной на векторах 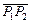и 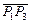, должен быть направлен вдоль оси x, так как вектор 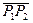лежит вдоль оси z, а вектор 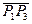лежит в плоскости yz. Этот вектор задается векторным произведением

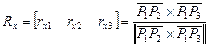
Наконец, вдоль оси Y должен быть направлен вектор, перпендикулярный к векторам R_x и R_z:

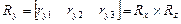
Искомая матрица преобразования есть

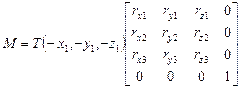
Проецирование

В настоящее время абсолютное большинство устройств вывода графической информации создают изображения на плоскости – экране монитора, бумаге и т.п. Несоответствие между объемными объектами и плоскими изображениями устраняется путем введения проекций, которые отображают трехмерные объекты на двумерной картинной плоскости.

Проекция объекта на картинную плоскость строится при помощи проецирующих лучей, которые выходят из одной точки (центра проекции) и проходят через каждую точку объекта. Пересечение этих лучей с картинной плоскостью и образует проекцию.

Далее рассматриваются различные виды проекций.

Для того, чтобы увидеть на плоскости монитора трехмерное изображение нужно уметь задать способ отображения трехмерных точек в двумерные. Сделать это можно, вообще говоря, по-разному. В общем случае проекции преобразуют точки, заданные в системе координат размерностью n в точки системы координат размерностью меньшей, чем n. В нашем случае точки трехмерного пространства преобразуются в точки двумерного пространства.

Проекции строятся с помощью проецирующих лучей или проекторов, которые выходят из точки, которая называется центром проекции. Проекторы проходят через плоскость, которая называется проекционной или картинной плоскостью, и затем проходят через каждую точку трехмерного объекта и образуют тем самым проекцию. Тип проецирования на плоскую, а не искривленную поверхность, где в качестве проекторов используются прямые. а не искривленные линии, называется плоской геометрической проекцией.

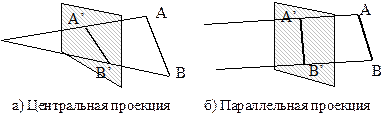
Рис 17. Плоские геометрические проекции

Плоские геометрические проекции делятся на два вида: центральные и параллельные. Если центр проекции находится на конечном расстоянии от проекционной плоскости, то проекция – центральная. Если же центр проекции удален на бесконечность, то проекция – параллельная.

В зависимости от удаленности центра проекции и взаимного расположения картинной плоскости, проецирующих лучей и осей координат выделяется несколько видов проекций. Сначала мы опишем аппарат параллельных проекций, затем опишем центральные проекции.