ВЕРТИКАЛЬНО ВБЛИЗИ ПОВЕРХНОСТИ ЗЕМЛИ
Задача 8.1. От карниза крыши с промежутком времени t0 = 1,0 с оторвались две капли. Определить расстояние между каплями спустя время t1 = 2,0 с после отрыва второй капли.
| t0 = 1,0 с t1 = 2,0 с | Решение. Запишем уравнения движения капель.
Пусть t0 = 0 – момент падения второй капли. Тогда координата второй капли в момент времени t равна 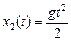 . Первая капля находилась в пути время (t + t0), поэтому . Первая капля находилась в пути время (t + t0), поэтому 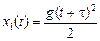 .
Расстояние между каплями в момент времени t = t1 равно .
Расстояние между каплями в момент времени t = t1 равно
|
| s = ? | |
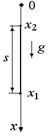 Рис. 8.1
Рис. 8.1
|
 =
= 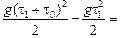
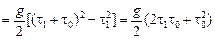 .
.
Итак,
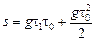 = 9,8 м/с2×1,0 с×2,0 с +
= 9,8 м/с2×1,0 с×2,0 с + 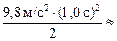 25 м.
25 м.
Заметим, что зависимость расстояния s между каплями от времени t имеет вид 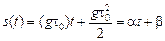 , где a = gt0, b=
, где a = gt0, b= 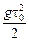 . Другими словами, расстояние между каплями изменяется по линейному закону, т.е. скорость удаления капель друг от друга постоянна. В самом деле: υ1(t) = g(t + t), υ2(t) = gt, υуд(t) = υ1(t) – υ2(t) = = g(t + t) – gt = gt0 = const.
. Другими словами, расстояние между каплями изменяется по линейному закону, т.е. скорость удаления капель друг от друга постоянна. В самом деле: υ1(t) = g(t + t), υ2(t) = gt, υуд(t) = υ1(t) – υ2(t) = = g(t + t) – gt = gt0 = const.
СТОП! Решите самостоятельно: В1–В4.
Задача 8.2.Из точек А и В, расположенных по вертикали (точка А выше) на расстоянии l = 100 м друг от друга, бросают одновременно два тела с одинаковой начальной скоростью υ0 = 10 м/с: из точки А – вертикально вниз, а из точки В – вертикально вверх (рис. 8.2). Через какое время и в каком месте они встретятся?
| l = 100 м υ0 = 10 м/с | Решение. Введём ось х, направленную вертикально вверх. Пусть начальная координата первого тела: x01 = l, а второго: х02 = 0. |  Рис. 8.2
Рис. 8.2
|
| tв = ? хв= ? | ||
Проекция начальной скорости на ось х для первого тела 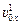 = –υ0, а для второго = –υ0, а для второго 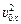 = +υ0. Проекция ускорения на ось х для обоих тел одинакова и равна: aх1 = ах2 = –g (см. рис. 8.2). Запишем кинематические уравнения движения для каждого тела: = +υ0. Проекция ускорения на ось х для обоих тел одинакова и равна: aх1 = ах2 = –g (см. рис. 8.2). Запишем кинематические уравнения движения для каждого тела:
|
первое тело х1(t) = х01 + 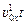 +
+ 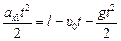 ;
;
второе тело х2(t) = х02 + 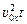 +
+ 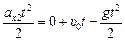 .
.
В момент встречи координаты тел равны:
х1(tв) = х2(tв) Þ 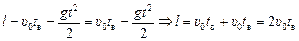 ,
,
отсюда
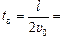 100 м : (2×10 м/с) » 5,0 с.
100 м : (2×10 м/с) » 5,0 с.
Читатель:Это какой-то странный результат: значение tв получилось бы точно таким же, если бы тела двигались навстречу друг другу равномерно со скоростями υ0 каждое. Выходит, что от ускорения 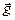 время встречи никак не зависит.
время встречи никак не зависит.
Автор: Да, не зависит. Если вдуматься, тут нет ничего удивительного, ведь ускорения обоих тел одинаковые, значит, за одинаковое время их скорости одинаково изменяются: Dυ1 = Dυ2 = gDt, а значит, друг относительно друга скорости тел в процессе движения не меняются.
Теперь найдём координату точки встречи, для этого достаточно подставить tв выражение для х1(t):
хв = х1(tв) = 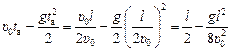 .
.
Читатель: Сразу видно, что мы где-то ошиблись.
Автор:Почему?
Читатель: Да потому, что
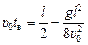 =
= 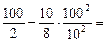 50 – 125 » –75 м,
50 – 125 » –75 м,
т.е. встреча должна произойти ПОД ЗЕМЛЕЙ!
Автор: Ну и что ж тут такого? Почему бы нам не представить себе, что вдоль оси х вырыт колодец? Вот в этом колодце на глубине 75 м тела и встретились бы через 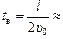 5,0 с.
5,0 с.
Ответ: 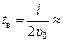 5,0 с; хв =
5,0 с; хв = 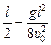 » –75 м.
» –75 м.
СТОП! Решите самостоятельно: В9–В11.
Задача 8.3. Два тяжелых шарика брошены с одинаковыми начальными скоростями из одной точки вертикально вверх, один через t секунд после другого. Они встретились в воздухе через Т секунд после вылета первого шарика. Определить начальную скорость шариков. Сопротивлением воздуха пренебречь.
| t T | Решение. Через время Т первый шарик окажется над землей на высоте h1, причем
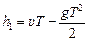 , ,
|
| υ0 = ? | |
где υ – начальная скорость шарика. Второй шарик к моменту времени Т находился в воздухе (Т – t) секунд, поэтому его высота h над землей будет
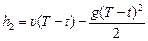 .
.
При встрече шариков h1 = h2, откуда
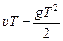
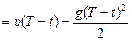 ,
,
 .
.
Отсюда 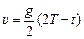 .
.
Ответ: 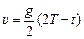 .
.
СТОП! Решите самостоятельно: В7, В8, С3.
Дата добавления: 2016-04-11; просмотров: 5918;
