При равно­переменном движении

Построение графиков зависимости

Координаты от времени

при равно­переменном движении

Задача 7.1. Даны три графика зависимостей υ_x = υ_x(t) (рис. 7.1). Известно, что х(0) = 0. Постройте графики зависимостей х = х(t).

Решение. Поскольку все графики – прямые линии, то движение по оси х равнопеременное. Так как υ_x возрастает, то а_х > 0.

В случае 1 υ_x(0) = 0 и х(0) = 0, поэтому зависимость х = х(t) совсем простая: х(t) = = 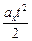. Поскольку a_х > 0 графиком х(t) будет парабола с вершиной в точке 0, ветви которой направлены вверх (рис. 7.2).

В случае 2 х(t) = υ_0xt + 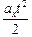– это также уравнение параболы. Выясним, где будет находиться вершина этой параболы. В момент t₁ (t₁ < 0) проекция скорости ме­няет свой знак: до момента t₁ υ_x < 0, а после момента t₁ υ_x > 0. Это значит, что до момента t₁ тело двигалось в отрицательном направ­лении оси х, а после момента t₁ – в по­ложительном направлении. То есть в момент t₁ тело совершило поворот. Следовательно, до момента t₁ координата х(t) убывала, а после момента t₁ x(t) стала

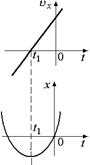Рис. 7.3

воз­растать. Значит, вершине параболы x = x(t) соответствует момент времени t1. Так как х(0) = 0, парабола х = х(t) проходит через точку 0 (рис. 7.3). В случае 3 υх меняет знак в момент t0 > 0. Этот момент времени со­ответствует вершине параболы x = x(t). Парабола проходит также через точку 0, поскольку х(0) = 0 (рис. 7.4).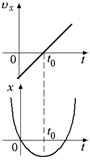

Рис. 7.4

Стоп! Решите самостоятельно: А2, В1, В2.

Задача 7.2.По данному графику υ_х = υ_х(t) (рис. 7.5) построить графики а_х(t) и х(t). Считать х(0) = 0.

Решение.

1. При t Î [0; 2] движение равноускоренное вдоль оси х без начальной скорости.

2. При t Î [2; 5] движение равномерное вдоль оси х.

3. При t Î [5; 6] движение равнозамедленное вдоль оси х. В момент t = 6 с тело останавливается, при этом а_х < 0.

4. При t Î [6; 7] движение равноускоренное в направлении, противоположном направлению оси х, a_х < 0.

На участке [0; 2] а_х = 1 м/с;

на участке [2; 5] а_х = 0;

на участке [5; 7]

а_х = –2м/с².

График а_х(t) представлен на рис 7.6.

Построим теперь график х = х(t).

На участке [0; 2] график х(t) представляет собой параболу с вершиной в точке 0. Значение х(2) = s₀₂ равно площади под графиком υ_х(t) на участке [0; 2], т.е. s₀₂ = 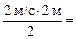2 м. Следовательно, х(2) = 2 м (рис. 7.7).

На участке [2; 5] движение равномерное с постоянной скоростью 2 м/с. График зависимости х(t) на этом участке – прямая. Значение х(5) = х(2) + s₂₅, где s₂₅ – путь, пройденный за время (5 с – 2 с) = 3 с, т.е. s₂₅ = (2 м/с)×(3 с) = 6 м. Следовательно, х(5) = = 2 м + 6 м = 8 м (см. рис. 7.7).

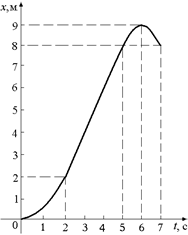
Рис. 7.7 Рис. 7.8

На участке [5; 7] а_х = –2 м/с² < 0, поэтому графиком х(t) является парабола, ветви которой направлены вниз. Вершина параболы соответствует моменту времени t = 6 с, так как υ_х = 0 при t = 6 с. Значение координаты х(6) = х(5) + s₅₆, где s₅₆ – путь, пройденный за промежуток времени [5; 6], s₅₆ = 1 м, следовательно, х(6) = 8 м + 1 м = 9м.

На участке [6; 7] координата х(t) убывает, х(7) = x(6) – s₆₇, где s₆₇ – путь, пройденный за промежуток времени [6; 7], s₆₇ = = 1 м, следовательно, х(7) = 9 м – 1 м = 8 м.

Окончательный график x = x(t) показан на рис. 7.8.

Стоп! Решите самостоятельно: А1 (б, в), В3, В4.

Правила построения графиков x = x(t)

по графикам υ_x = υ_x(t)

1. Необходимо разбить график υ_х = υ_х(t) на участки так, чтобы на каждом участке выполнялось условие: a_х = const.

2. Учесть, что на тех участках, где a_х = 0, график x = x(t) – прямая, а там, где a_х = const ¹ 0, графиком x = x(t) является парабола.

3. При построении параболы учесть, что: а) ветви у параболы направлены вверх, если а_х > 0 и вниз, если а_х < 0; б) координата t_в вершины параболы находится в той точке, в которой υ_х(t_в) = 0.

4. Между участками графика x = x(t) не должно быть изломов.

5. Если известно значение координаты в момент t₁ x(t₁) = х₁, то значе­ние координаты в момент t₂ > t₁ определяется по формуле x(t₂) = х₁ + s⁺ – s^–, где s⁺ – площадь под графиком υ_х = υ_х(t), s^– – площадь над графиком υ_х = υ_х(t) на участке [t₁, t₂], выраженные в единицах длины с учетом масштаба.

6. Начальное значение координаты х(t) должно быть задано в условии за­дачи.

7. График строится последовательно для каждого участка, начиная с точки t = t₀, линия x = x(t) – всегда непрерывная, поэтому каждый следующий участок начинается в той точке, где оканчивается предыдущий.

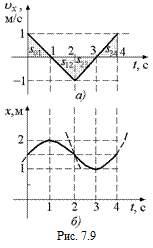
Задача 7.3.По данному графику υ_х = υ_х(t) (рис. 7.9,а) построить график x = x(t). Известно, что х(0) = 1,5 м.

Решение.

1. График υ_х = υ_х(t) состоит из двух участков: [0; 2], на котором a_х < 0 и [2; 4], на котором а_х > 0.

2. На участке [0; 2] график x = x(t) – это парабола, ветви которой направлены вниз, так как а_х < 0. Координата вершины t_в = 1 с, так как υ_х(1) = 0, х(1) = х(0) + s₀₁ = = 1,5 м + 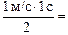2,0 м. Парабола пересекает ось х в точке х = 1,5 м, так как x(0) = 1,5 м по условию задачи (рис. 7.9,б).

3. На участке [2; 4] графиком x = x(t) также является парабола, но ветвями вверх, так как а_х > 0. Ее вершина находится в точке t_в = 3с, так как υ_х(3) = 0.

Значения координаты х в моменты времени 2с, 3с, 4с легко найти:

х(2) = х(1) – s₁₂ = 2 м – 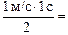1,5 м;

х(3) = х(2) – s₂₃ = 1,5 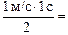м – 1 м;

х(4) = х(3) + s₃₄ = 1 м + 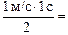1,5 м.

Стоп! Решите самостоятельно: А1 (а), В5 (д, е, ж).

Задача 7.4.По данному графику x = = x(t) построить график υ_х = υ_х(t). График x = x(t) состоит из частей двух парабол (рис. 7.10,а).

Решение.

1. Отметим, что в момент t = 0 υ_х < 0, так как х убывает;

в момент t = 1 с υ_х = 0 (вершина параболы);

в момент t = 2 с υ_х > 0, так как х растет;

в момент t = 3 с υ_х = 0 (вершина параболы);

в момент t = 4 с υ_х < 0, так как х убывает.

2. Поскольку график x = x(t) состоит из парабол, движение на каждом участке [0; 2] и [2; 4] равнопеременное и а_х = const на каж­дом участке. Следовательно, график υ_х = υ_х(t) со­стоит из двух прямолинейных участков, причем в пределах каждого участка [0; 2] и [2; 4] наклон графиков υ_х = υ_х(t) к оси t не меняется.

3. График υ_х = υ_х(t) – непрерывный, но может иметь изломы.

4. Найдем значение υ_х(0). Поскольку на участке [0; 1] координата х(t) убывает от 0 до –1 м, то путь, пройденный за промежуток времени [0; 1], составит s₀₁ = 1 м. С другой стороны, этот путь равен площади над графиком υ_х = υ_х(t) на участке [0; 1]: 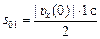, отсюда 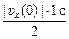= 1 м, |υ_x(0)| = 2 м/с.

Поскольку на участке [0; 1] тело движется в направлении, противоположном направлению оси х, то υ_х(0) < 0, отсюда υ_х(0) = = –|υ_x(0)| = –2 м/с.

Следовательно, график υ_х = υ_х(t) на участке [0; 1] – это отрезок прямой, проходящей через точки (0; –2) и (1; 0). Из построения получаем, что υ_х(2) = +2 м/с.

5. Так как υ_х = υ_х(t) – непрерывная функция, а υ_х(2) = 2 м/с, то график на участке [2; 4] начинается из точки с координатами (2; 2). Вторая точка, через которую пройдет график υ_х = υ_х(t) на участке [2; 4], – это точка с координатами (3; 0), так как υ_х(3) = 0. Из построения по­лучаем, что υ_х(4) = –2 м/с.

График υ_х(t) приведен на рис. 7.10.б.

Стоп! Решите самостоятельно: В6, Г2, Г3 (а,б).