Вынужденные колебания подрессоренной и неподрессоренных масс двухосного автомобиля с учетом затухания (подвеска с амортизатором в движении)
По-прежнему рассматриваем автомобиль, у которого взаимное влияние подрессоренных масс не велико т.е. εу ≈ 1,что позволяет рассматривать только одну из подвесок, не обращая внимания на влияние другой.
В первом приближении представим неровности дороги в синусоидальном виде (любые вынужденные колебания можно разложить в гармонический ряд).
Допустим, что контакт колеса с дорогой происходит только в одной точке (справедливо для небольших неровностей, которые автомобиль обычно переезжает на большой скорости – это, собственно, нас и интересует). Тогда текущая координата волны, в которой происходит контакт колеса с дорогой обозначим q:
,
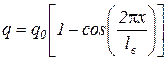q0 – амплитуда волны; х – абсцисса точки с вертикальной координатой q; lв – длина волны.
При равномерном движении х = V·t получим:
,
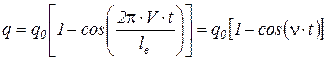где v = 2π·V/lв – частота возмущающей силы
В § 10.5 мы получили мат. модель затухающих колебаний подвески:
.
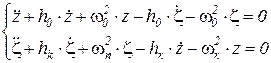Для проведения анализа упростим модель – избавимся от одной из степеней свободы путем приведения жесткостей упругих элементов, допустив независимость колебаний масс mп и mн:
.
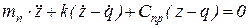Подставим q и приведем уравнение к каноническому виду:
,
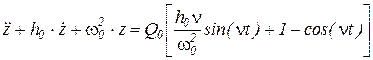где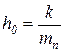 
; 
; 
.
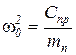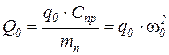Общее решение найдено как сумма решений однородного (левая часть) уравнения и частного решений:
.
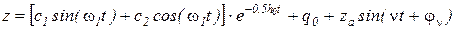Часть I – затухающие колебания. Часть II – не затухающие, установившие колебания. Частью I можно пренебречь.
Тогда после преобразования получим
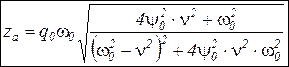– мат. модель установившихся вынужденных колебаний;
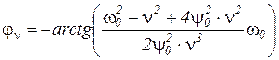– фазовый угол.
Проведем анализ.
Для удобства заменим zv = za/q0 , тогда
.
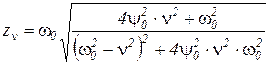Зависимость амплитуды колебаний подрессоренной массы от частоты вынуждающей силы имеет две характерные резонансные точки: v = ω0 и v = ωк. При отыскании решения мат модели мы допустили независимость колебаний масс mп и mн. Это справедливо лишь для v =(0…0,5) ωк. Тогда, учитывая ω0 << ωк первый резонанс мы можем достоверно анализировать по зависимости zv.
При v = ω0 получим
.
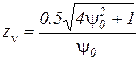Мы знаем, что ψ0 = 0,15…0,25. Тогда zv = 3,48 … 2,23.
При v = ωк зависимость zv существенно занижает результат. Для корректировки zv нужно умножить на коэффициент:
.
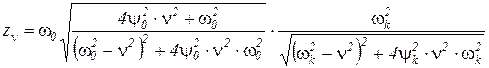Поправочный коэффициент при v = ωк имеет вид 1/(2·ψk ·v).
Учитывая ψk = 0,25…0,45, получим поправочный коэффициент 2/ωk … 1,11/ ωk.
– Амплитудно-частотная характеристика грузового автомобиля (АЧХ)
Итак,
Исходные данные, необходимые для составления АЧХ: ω0, ωк, ψ0, ψк:
ω0, ωк – парциальные частоты колебаний подрессоренной и неподрессоренной масс:
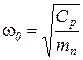и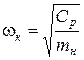 
;
Ср, mп, mн – жесткость рессоры и соответствующие массы;
ψ0, ψк – относительный коэффициент затухания колебаний подрессоренной и неподрессоренной масс:
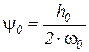и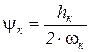 
;
h0, hк – парциальные коэффициенты сопротивления подвеск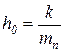и:
и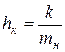 
;
К – коэффициент неупругого сопротивления подвески (коэффициент рассеяния энергии).
ВЫВОДЫ
1. Установившиеся (без учета части I, см. мат. модель выше) вынужденные колебания происходят с частотой возмущающей силы. Частота от наличия амортизатора и его характеристик не зависит.
2. Амплитуда установившихся вынужденных колебаний не зависит от времени и от начальных условий. Наличие амортизатора не делает колебания затухающими, а амплитуда колебаний с течением времени не меняется.
3. Амплитуда установившихся вынужденных колебаний подрессоренной массы зависит от соотношения между собственной частотой Ω0 (≈парциальной ω0) и частотой возмущений v.
4. Наибольшая амплитуда колебаний достигается при резонансе. Частота низкочастотного резонанса чуть меньше ω0 – менее чем на 1 %. Наличие амортизатора несколько увеличивает этот процент.
5. Амортизатор создает смещение фаз перемещений относительно вынуждающей силы, причем величина сдвига зависит от вынуждающей частоты.
6. Амортизатор уменьшает все амплитуды: перемещений, виброскоростей и виброускорений (увеличение ψ0 в интервале 0,2 …0,4 уменьшает z и z`` почти в два раза).
7. Из АЧХ видно, что:
a. амплитуда колебаний подрессоренной массы имеет один экстремум – при низкочастотном резонансе;
b. амплитуда колебаний неподрессоренной массы имеет 2 экстремума – при низкочастотном и высокочастотном резонансе;
c. амплитуда виброускорений подрессоренной массы также имеет 2 экстремума, смещенных по фазе относительно колебаний неподрессоренной массы.
Частота возмущений зависит от скорости автомобиля и длины l
Дата добавления: 2016-03-15; просмотров: 1538;