Свободные колебания массы на упругом элементе

Рассмотрим свободные (т.е. после(!) возбуждающего толчка) колебания массы.

Сила, развиваемая упругим элементом, пропорциональна его жесткости и прогибу: .

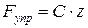Сила инерции, действующая на массу, пропорциональна ускорению: 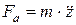(точки над переменной означают производную по времени).

В статическом состоянии имеем: 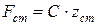(F_ст численно равна mg).

Баланс сил имеет вид:

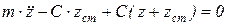или .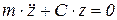

Приведем уравнение к каноническому виду (т.е. старшая производная должна быть без коэффициентов):

.

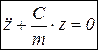Обозначим С/m = ω² (где ω – собственная частота системы), тогда

.

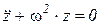Характеристическое уравнение имеет вид:

К² + ω² =0; К² =– ω²; К = i· ω

Решение дифференциального уравнения ищем в виде:

.

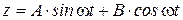Из начального условия известно, что при t = 0 и z = 0. Откуда B = 0.

Тогда

. . . .

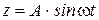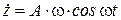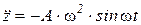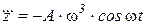Приведение жесткостей упругого элемента и шины:

Деформация подвески складывается из деформаций шины и пружины под действием внешней силы (подрессоренной массы, неподрессоренную не учитываем):

;

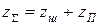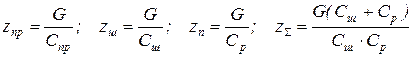
Тогда окончательно получим: .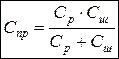

8.3. Свободные колебания подрессоренной массы двухосного автомобиля без учета затухания и влияния неподрессоренных масс (масса на 2^х пружинах)

После таких допущений остается 2 степени свободы: вертикальное перемещение z₀ и поворот α в продольной вертикальной плоскости. Оба эти движения вызывают изменение прогибов z₁ и z₂ упругих элементов и возникновению сил С_пр1·z₁ и С_пр2·z₂ действующих со стороны этих элементов на подрессоренную массу.

Уравнения сил и моментов запишутся следующим образом:

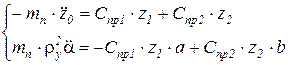
где 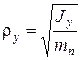– радиус инерции подрессоренной массы относительно поперечной оси ОУ; J_y – момент инерции подрессоренной массы относительно той же оси; a_п и b_п – расстояние от передней и задней осей до центра подрессоренной массы.

Выразим z₀ и α через координаты z₁ и z₂:

Из прямоугольного треугольника АВС

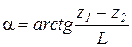или для малых углов в рад ^*;

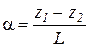Из того же треугольника

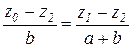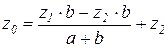è 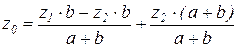è è

.

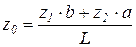Подставим вторые производные в систему:

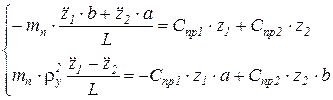
Обе части первого уравнения умножим на b, а левую часть перепишем:

,

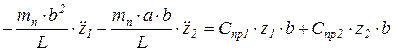затем вычтем из второго уравнения и упростим

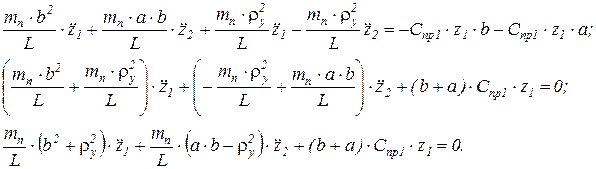
Вновь первое уравнение системы умножим теперь на а

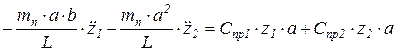
затем сложим со вторым уравнением системы и упростим

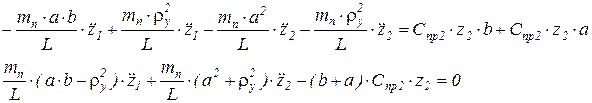
Приведем систему к каноническому виду:

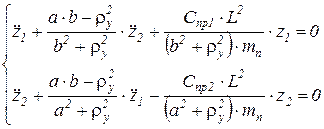
Введем обозначения:

;

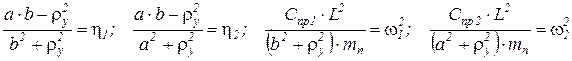Тогда система примет вид:

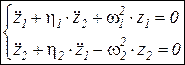– мат. модель колебания массы на двух упругих элементах без амортизаторов

Система является «связанной», т.к. в каждое из уравнений входят два ускорения по z₁ и z₂. Это проявляется в том, что колебания передней и задней части автомобиля представляет собой сумму двух синусоидальных колебаний с различными амплитудами и частотами, зависящими от параметров обеих подвесок.

После решения получим низкую и высокую собственные частоты системы:

.

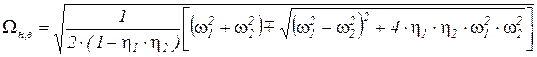Если 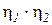= 0, то 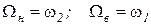– гармонические колебания точки В и А соответственно. Чем больше 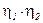, тем больше взаимное влияние подвесок. 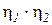= 0, если .

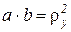Вводят коэффициент распределения подрессоренных масс .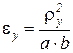

Для большинства полностью груженых автомобилей (легковых и грузовых) 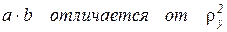не более 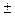20 %.

Если ε_у =0,8…1,2, то собственные частоты подвесок (в данном случае равные парциальным^*) можно найти следующим образом

.

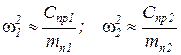^*Парциальная частота – это частота колебаний сложной системы, если все степени свободы, кроме одной, устранены.