Свободные колебания подрессоренной и неподрессоренных масс двухосного автомобиля с учетом затухания (подвеска с амортизатором)

Подвеска реального автомобиля (как колебательная система) имеет упругий элемент (рессору, пружину) и целый ряд демпферов (трение во втулках сайлентблоков, между листами рессоры, внутреннее трение (нагрев) шин и т.д. и т.п.). Поэтому колебания подвески даже без амортизатора являются затухающими. Однако рассеяние энергии в амортизаторе существенно больше, поэтому будем учитывать только его.

По-прежнему рассматриваем автомобиль, у которого взаимное влияние подрессоренных масс не велико т.е. ε_у ≈ 1,что позволяет рассматривать только одну из подвесок, не обращая внимания на влияние другой.

В первом приближении будем считать, что сила сопротивления амортизатора линейно зависит от скорости его работы ( 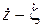). Тогда движение подрессоренной массы опишем уравнением:

;

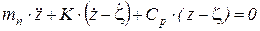Движение неподрессоренной массы:

.

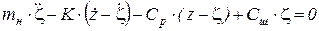К – коэффициент неупругого сопротивления подвески (коэффициент рассеяния энергии), Н·с/м (численно равен силе сопротивления амортизатора при скорости движения штока 1 м/с).

Приведем оба уравнения к каноническому виду. При этом введем замену 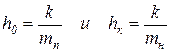, которые назовем парциальными коэффициентами сопротивления подвески (с^-1), также подставим парциальные частоты:

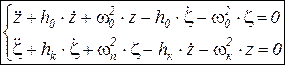– мат.модель затухающих колебаний подвески.

Учитывая слабую связанность колебательных процессов (из-за существенной разницы жесткостей шины и рессоры) последними двумя членами в обоих уравнениях можно пренебречь. Тогда характеристические уравнения уравнений и его корни (для положительного дискриминанта) будут иметь вид:

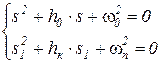è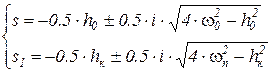

Таким характеристическим уравнениям соответствуют следующие решения:

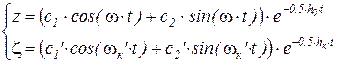
где 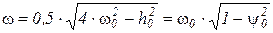– частота колебаний подрессоренной массы с учетом затухания; 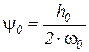– относительный коэффициент затухания колебаний подрессоренной массы; 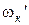и ψ_к – то же для неподрессоренной массы.

Константы с₁, с₂, 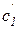и 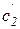зависят от начальных условий.

Произведем замену

,

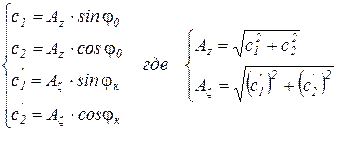где φ₀ и φ_к – начальный фазовый угол колебаний соответственно подрессоренной и неподрессоренной масс; А_z, 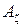– начальная амплитуда колебаний соответственно подрессоренной и неподрессоренной масс

После подстановки в решение получим

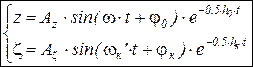– мат. модель затухающих колебаний подвески.

Экспонента характеризует затухание колебаний. Величина е^х определяет знаменатель р геометрической прогрессии.

Затухание за один период 2π характеризуется логарифмическим декрементом затухания δ:

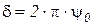. (е^δ – (просто) декремент затухания).

У современных автомобилей ψ₀ = 0,15…0,25; ψ_к = 0,25…0,45.

У гидропневматической подвески ν = 0,5…0,8 Гц, поэтому задают ψ₀ = 0,6…0,4.

Пример: относительный коэффициент затухания колебаний подрессоренной массы ψ₀=0,2; тогда логарифмическим декрементом затухания δ = 2·π·0,2 = 1,2566; знаменатель прогрессии р = е^1,2566 = 3,5136. Т.е. через один цикл колебания амплитуда уменьшится в 3,5136 раза. После второго колебания – в 3,5136² раза и т.д.