КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

Хотя при рассмотрении с близкого расстояния Земля выглядит относительно плоской, мы все знаем, что она имеет приблизительно сферическую форму Карты, как мы видели, - сокращение реальности, они придуманы для того, чтобы представлять не только объекты на ее поверхности, но и форму Земли. Глобус — традиционный способ отображения формы Земли. Хотя глобусы в целом передают форму Земли и показывают пространственные очертания объектов размером с континент, их довольно трудно носить в кармане, даже при очень мелком масштабе (даже при 1:100'000'000). Большинство тематических карт, с которыми нам приходится сталкиваться на практике, в географическом анализе, имеют значительно более крупный масштаб, где-то от 1:ГООО'000 до 1:1000, в зависимости от уровня детализации. Глобус такого размера было бы трудно и дорого делать и еще более трудно переносить или разворачивать на столе дигитайзера (digitizing table) для ввода в ГИС. Поэтому картографы разработали набор методов, называемыхкартографическими проекциями (тар projections), которые предназначены для изображения с приемлемой точностью сферической Земли на плоском носителе. В буквальном смысле, процесс создания проекции представляется как помещение источника света внутри прозрачного глобуса, на котором размещаются непрозрачные земные объекты, и проецирование их контуров на двухмерную поверхность, окружающую глобус.

Возможны разные виды проецирования при окружении глобуса цилиндром, конусом и даже помещении возле него плоского листа бумаги. Каждый из этих методов, как первоначально представлялось, создает так называемоесемейство проекций (projection family). Поэтому существуют семействопланарных (planar) проекций, семействоцилиндрических(cylindrical) проекций и семействоконических (conical) проекций (Рисунок 3.4). Существует еще четвертое семейство проекций, называемых азимутальными (azimuthal), они основаны на идее проецирования параллельными лучами света на плоский материал; мы их рассмотрим чуть позже. Сегодня процесс проецирования сферической поверхности на плоский носитель выполняется с использованием методов геометрии и тригонометрии, которые воспроизводят физический процесс проецирования света через глобус.

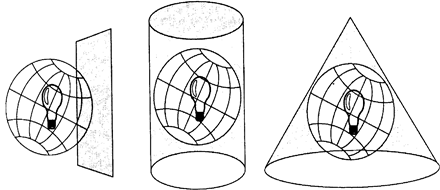
Рисунок 3.4. Три семейства картографических проекций. Они могут создаваться с использованием: а) плоских поверхностей, b) цилиндров, с) конусов.

Картографы разработали и другие проекции для лучшего представления Земли на плоском материале. К сожалению, многие из тех в географическом сообществе, кто не является картографом, по большей части пренебрегали этим важным аспектом представления пространства. Причины этому кроются в истории и философии географии. Но с распространением спутникового дистанционного зондирования и географических информационных систем этим вопросом нельзя пренебрегать и дальше. Он тем более значим сегодня, поскольку существует потребность в минимизации искажающих эффектов проекций при представлении пространственных феноменов, плюс широкий спектр картографической информации, с которой географу каждый день приходится иметь дело за компьютером. Эти вопросы оказывают воздействие на все подсистемы ГИС и должны быть хорошо поняты, дабы ограничить их негативное влияние.

Проекции - не абсолютно точные представления географического пространства. Каждая создает свой набор типов и величин искажений на карте. Важные характеристики карт, которые должны сохраняться для точных аналитических операций, часто определяют выбор той или иной проекции. Эти характеристики включают углы (или формы), расстояния, направления, площади объектов. При выполнении проекции невозможно сохранить все эти характеристики одновременно. Мы рассмотрим каждую из них в отдельности, но сначала нам нужно установить некоторую полезную терминологию, помогающую нам понимать изменения характеристик в процессе проецирования.

Упрощенно, процесс проецирования представляется двумя этапами: вначале преобразуют земной шар впромежуточный глобус (reference globe) в зависимости от выбранного масштаба; затем этот глобус проецируется на плоскую поверхность [Robinson et al., 1995]. Численный масштаб первого преобразования называетсяглавным, или общим, масштабом (principal scale), он равен отношению радиуса промежуточного глобуса к радиусу земного шара. Таким образом мы имеем численный масштаб, постоянный по всей поверхности этого глобуса, поскольку его форма повторяет форму земного шара.

Перед тем, как сделать второй шаг, отметим, чтомасштабный коэффициент(scale factor), называемый также относительным масштабом, определяемый как частное отделения местного масштаба (actual scale) на общий масштаб, по определению равен единице по всей поверхности промежуточного глобуса. Когда же мы переходим от его сферической поверхности к двухмерной карте, относительный масштаб обязательно изменится, поскольку плоская и сферическая поверхности не совместимы. Следовательно, масштабный коэффициент будет разным в разных точках карты [Robinson et al., 1995]. Нам нужно постоянно помнить об изменяющемся масштабном коэффициенте, когда мы рассматриваем различные виды искажений, возникающих при проецировании.

На поверхности глобуса направления сторон света всегда отстоят от соседних на 90°. То есть, например, между севером и востоком всегда прямой угол. Это соотношение углов может сохраняться и на картографической проекции. Проекции, сохраняющие это свойствоуглового соответствия(angular conformity), называютсяконформными, илиравноугольными(conformal, orthomorphic), картографическими проекциями. Конформные проекции позволяют нам математически организовать сжатия и растяжения на карте так, чтобы масштабный коэффициент не зависел от направления в каждой ее точке. При этом масштабный коэффициент не будет равен единице в каждой точке карты, а параллели и меридианы в полученной карте всегда будут проходить под прямыми углами друг к другу, как они и были на глобусе, однако площади объектов будут искажены [Robinson et al., 1995]. Запомните, что сохранение углов труднодостижимо для больших участков земной поверхности и этого разумно добиваться лишь для малых участков.

Конформные проекции искажают площади, что делает измерения площадей на карте некорректными. Но мы можем сохранить площади, используяравновеликие, или равноплощадные, проекции (equal area or equivalent projections), в которых произведение масштабных коэффициентов по главным направлениям горизонта равно единице [Robinson et al., 1995]. Это условие гарантирует, что если вы, например, считаете площади квадратных объектов на карте, то произведение их двух сторон даст тот же результат, что и при подсчете на промежуточном глобусе. Это обусловлено тем, что произведение масштабных коэффициентов по этим двум направлениям равно единице. Однако, при достижении этой идентичности мы обнаруживаем, что масштабный коэффициент будет разным по разным направлениям для всех точек карты, кроме точек, лежащих на особых линиях проекции. Другими словами, сохраняя площади, мы искажаем углы. Таково фундаментальное соотношение этих двух параметров для проецированных карт — нельзя одновременно сохранять и площади и углы.

Если целью проецирования карты является измерение расстояний, то нам следует выбрать проекцию, сохраняющую расстояния. Такие проекции, называемыеравнопромежуточными, или эквидистантными (equidistant projections), требуют сохранения масштаба карты постоянным; он должен быть таким же, как и главный масштаб промежуточного глобуса [Robinson et al., 1995]. Существуют два способа добиться этого. Первый сохраняет масштабный коэффициент равным единице вдоль одной или более параллельных линий, называемыхстандартными параллелями (standard parallels). Расстояния, измеренные вдоль этих линий, будут соответствовать реальным. Другой подход заключается в сохранении единичного масштабного коэффициента вдоль всех направлений из одной точки, либо из двух. Расстояния, измеренные от таких точек по любому направлению, будут точно представлять реальные. Но для любых других точек это не будет соблюдаться. Как вы понимаете, здесь очень важен выбор таких точек. Обычно выбирается та точка, от которой производится большинство измерений.

Когда карты используются для навигации, наибольший интерес представляет сохранение направлений. Сохранение истинных направлений ограничено сохранением дуг окружностей больших кругов, которые определяют кратчайшее расстояния между двумя точками на поверхности Земли. Обычно нашей целью является отображение маршрутов этих больших кругов как прямых линий. Есть два основных способа сделать это. Первый используется для малых областей, в которых большие круги отображаются практически прямыми линиями между всеми точками области. Однако, если вы пересекаете с ними меридиан, то угол пересечения будет неправильным. Как ограниченная площадь, так и неточность углов пересечения меридианов и больших кругов, существенно ограничивают использование этой проекции для данных целей. Альтернативный вариант, называемыйазимутальной проекцией, более широко используется для сохранения направлений. Как и в случае эквидистантной проекции мы выбираем одну или две точки, из которых будут сохраняться направления. В этом случае прямые линии, проведенные из этих точек, будут соответствовать истинным направлениям. Опять же, направления из любых других точек не будут соответствовать реальности.

Позднее мы обсудим проблему смешивания разных проекций внутри одной геоинформационной системы, особенно при вводе, но пока нам нужны некоторые практические правила для определения того, какие из множества картографических проекций нам подошли бы в зависимости от видов выполняемого анализа. Если анализ требует отслеживания движения или изменения направлений движения объектов, например, при использовании телеметрии для регистрации положений каждого члена стада северных оленей в разное время, то наиболее подходящей будет конформная проекция. Этот вид проекций также больше всего подходит для производства навигационных карт и когда важна угловая ориентация, как часто бывает с метеорологическими или топографическими данными. Эта группа проекций включает проекцииМеркатора, поперечную Меркатора, коническую конформную Ламберта и конформную стереографическую.

Общегеографические и учебные карты чаще всего требуют использования равновеликих проекций, но наш интерес - анализ. Как говорит название, такие карты больше всего подходят, когда среди вычислений преобладают вычисления площади. Например, если вы заняты расчетом изменения соотношений разных видов растительного покрытия земли со временем, или если вы исследуете некоторую местность на предмет достаточной площади для размещения торгового комплекса, то равновеликие проекции подойдут лучше других.

Рассматривая использование равновеликих проекций, вам необходимо учитывать размер интересующей территории, а также величину и распределение угловых искажений. Небольшие участки отображаются с гораздо меньшими угловыми искажениями при использовании равновеликих проекций, что может быть полезно, когда важны и площади и формы. С Другой стороны, чем больше площадь изучаемой территории, тем более точны ее измерения при использовании равновеликой проекции, по сравнению с проекциями других типов. Для среднемасштабных карт наиболее часто встречаются равновеликая проекция Альберта и равновеликая проекция Ламберта.

Проекты, в которых требуется определение кратчайших маршрутов, особенно на длинные дистанции, нуждаются в азимутальных проекциях, поскольку в них возможно изображение больших кругов как прямых линий. Эти проекции чаще всего используются на картах воздушного сообщения, радиопеленгации, слежения за спутниками и картографирования других небесных тел [Robinson et al., 1995]. Эти проекции стали популярны лишь недавно, но их использование будет расти с расширением использования ГИС в этих областях. Наиболее часто вам будут встречаться такие азимутальные проекции какравновеликая Ламберта, стереографическая, азимутальная эквидистантная, ортографическая и гномоническая проекции. Отметим, что некоторые из них сохраняют как направления, так и площади. Это свойство может оказаться полезным для анализа крупных атмосферных явлений, таких как дымовые следы вулкана, которым свойственно двигаться по маршруту большого круга по мере рассеивания в атмосфере и движения по общим правилам циркуляции на Земле.

Есть много проекций для выбора - гораздо больше, чем перечислено здесь. Некоторые специальные проекции особенно подходят для отображения всей Земли или очень больших ее участков. Другие позволяют лучше координировать крупные картографические программы, такие как создание топографических карт целого континента, которое выполняется небольшими порциями. Список велик. Как вы увидите позднее, выбор проекции — один из основных процессов создания ГИС. Вам следует потратить время на выбор хорошего справочника по картографическим проекциям, с особым вниманием к тому, какие параметры каждая из них сохраняет. С нашей точки зрения могут оказаться полезными две книги: [Nyerges and Jankowski, 1989] и хорошо известный справочник [Snyder, 1988; есть более современное издание].