Способ параллельного перемещения

Для параллельного перемещения (переноса) справедливо утвержде­ние, которое может быть выражено в виде следующей теоремы:

при параллельном переносе геометрической фигуры относительно плоскости проекции проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

Докажем эту теорему для случая, когда проецируемая фигура плос­кая и ее плоскость принадлежит плоскости уровня , плоскость a || (рис. 2). В этом случае на основании инвариантного свойства 2д (см. § 6) /1/ горизонтальная проекция Ф' будет конгруэнтна самой фигуре Ф (Ф' Ф).

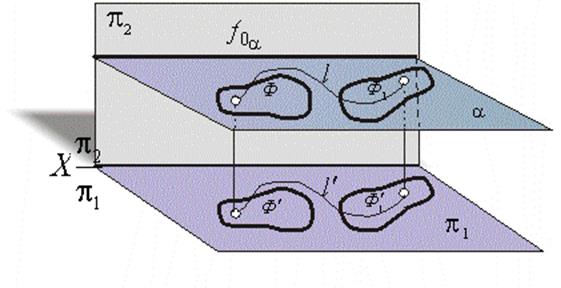
Рис.2

При перемещении фигуры Ф в новое положение Ф₁, фигура Ф₁ бу­дет конгруэнтна Ф, так как:

а) расстояние между точками фигуры не меняется;

б) в процессе перемещения фигура Ф все время остается в плоскости a .

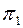
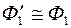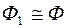В силу параллельности плоскостей a и , но , а 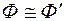, следовательно, 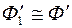. Доказанная теорема будет справедли­ва и в случае, когда геометрическая фигура занимает произвольное положение относительно плоскости проекции.

Отметим еще два свойства параллельного перемещения:

1. При всяком перемещении точки в плоскости, параллельной плоскости проекции 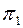, ее фронтальная проекция перемещается по пря­мой, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости, параллельной 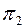, ее горизонтальная проекция перемещается по прямой, па­раллельной оси х.

Справедливость отмеченных свойств может быть легко показа­на на простом примере.

Возьмем плоскость a, параллельную горизонтальной плоскости проекции 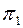, (рис. 3). Пусть точка 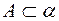переместится из положения А в 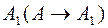, двигаясь в плоскости a, по произвольной траектории (l₁ , l ₂ или l₃). Очевидно, фронтальная проекция точки 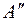переместится в 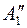, при этом 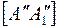принадлежит следу 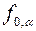, который параллелен оси х 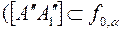|| x).

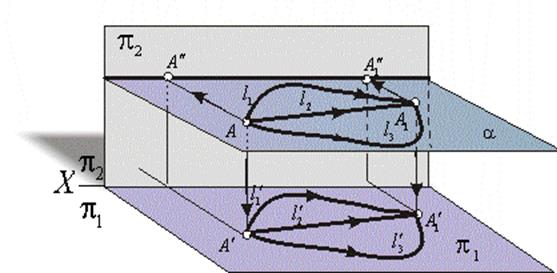Рис.3

Если точка будет перемещаться параллельно плоскости , то горизонтальная проекция траектории перемещения точки из перво­начального положения в новое представляет собой отрезок параллельный оси x и не

зависит от вида линии — траектории перемещения точки из одного положения в другое.

Пользуясь приведенной теоремой и отмеченными свойствами, легко построить новые проекции геометрической фигуры по заданным ее ортогональным проекциям, и, в частности, такие ее проекции, которые соответствуют отмеченным выше положениям проецируемой фигуры по отношению к плоскости проекции.

Проследим на примерах использование способа параллельного перемещения для перевода произвольно расположенной геометрической фигуры в частное положение.

ПРИМЕР 1. [АВ] прямой общего положения, а перевести в положение, парал­лельное плоскости (рис. 4)-задача 1.

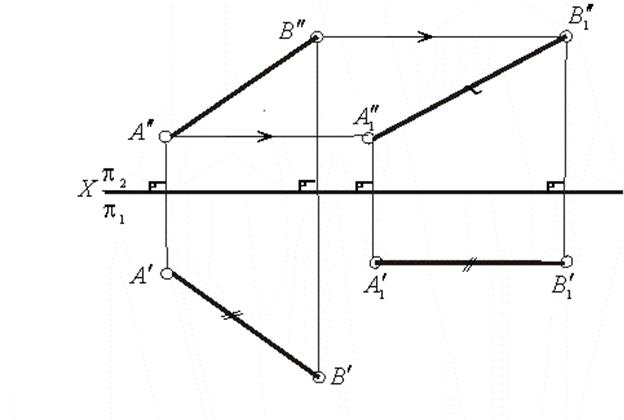
У [АВ], параллельного плоскости , горизонтальная проекция должна быть параллельна оси х. Поэтому переводим 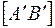в новое положение 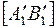, парал­лельное оси х. Перемещение отрезка в новое положение осуществляем так, что­бы любые его точки двигались в плос­костях, параллельных плоскости 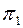. При таком перемещении новая горизонталь­ная проекция конгруэнтна исходной .

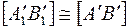Рис. 4

Фронтальные проекции точек отрезка [A"В"] будут перемещаться в новое положение по прямым, параллельным оси х (свойство 1, с.49 /1/).

На рис. 4 графические построения выполнены в указанной ниже последо­вательности:

1) через произвольную точку 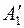про­вели прямую 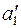, параллельную оси х;

2) отложили на ней от точки 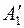, отрезок ;

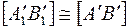3) из точек 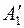и 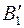восставили пер­пендикуляры к оси x: и нашли точки пе­ресечения их с соответствующими гори­зонтальными прямыми, проведенными через точки А" и В".

Полученные точки 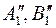являются концами фронтальной проекции отрезка 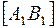, параллельного плоскости .

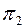Для перевода отрезка прямой, произвольно расположенной в про­странстве, в положение, параллельное плоскости 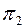, потребовалось выполнить только одно перемещение отрезка параллельно плоскос­ти проекции. Для перевода отрезка из общего положения в проецирующее необходимо последовательно выполнить два его перемещения параллельно плоскостям проекции: вначале перевести отрезок в положение, параллельное плоскост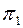и (или 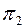) путем перемещения параллельно плоскост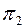и (или 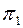), затем перевести отрезок в положе­ние, перпендикулярное 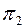(или ).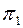

ПРИМЕР 2. 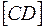прямой общего положения b перевести в положение 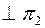(рис.5). На рис.5 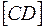вначале переведен в положение || 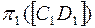- задача 1, затем перемещением параллельно плоскости 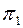— в положение 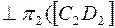)- задача 2..

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проеци­рующее, можно легко перевести плоскость, произвольно распложенную в пространстве, в частное положение (параллельное или перпендикуляр­ное плоскости проекции).

На рис. 6 показан перевод плоскости общего положения 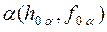вновое 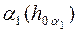, при этом .

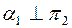Как видно из чертежа, перевод плоскости aв положение a₁ осу­ществлен с помощью горизонтали h, которая переведена в положе­ние 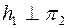, поэтому и 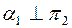. Следует обратить внимание на то, что расстояние d остается постоянным:

.

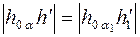Рис. 7 дает представление о преобразовании ортогональных проек­ций 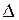ABC, определяющего плоскость общего положения b, в проекции 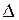А₂В₂С₂, задающего плоскость .

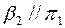Геометрические построения выполнены в последовательности, ука­занной индексами, поставленными у проекций точек справа внизу. Выполненные на эпюре построения соответствуют перемещению плоско­сти в пространстве вначале || 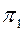во фронтально-проецирующее положение ( 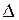А₁В₁С₁)- задача 3, затем перемещением || 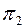плоскость треугольника переве­дена в положение || 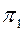( 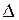А₂В₂ С₂)-задача 4.

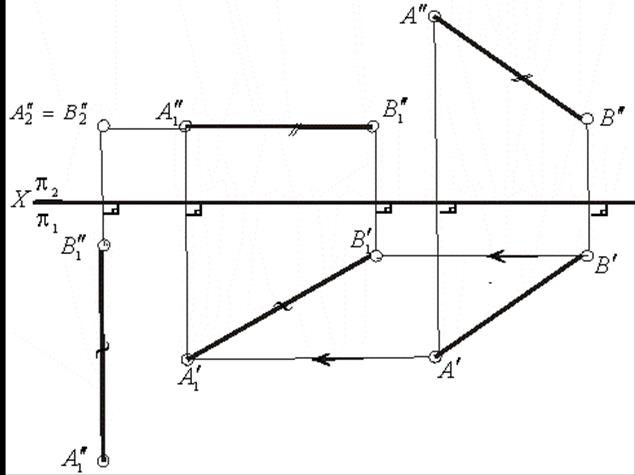
Рис.5

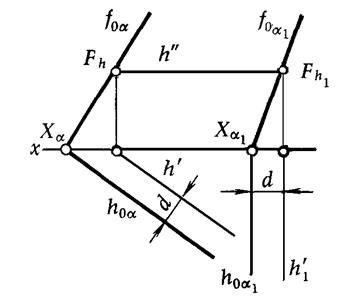Рис.6

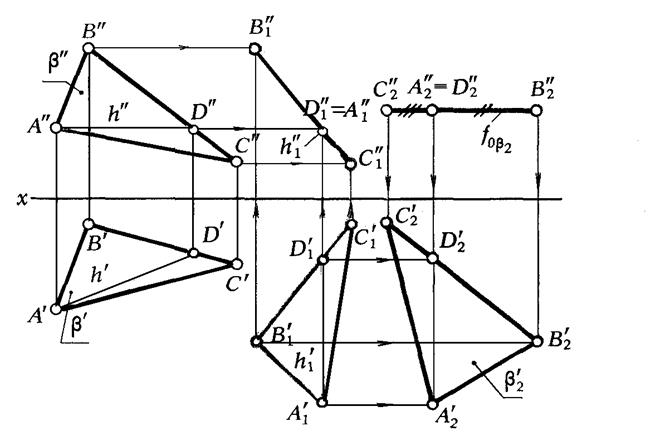
Рис.7