Перпендикулярной к плоскости проекции
Вращение вокруг оси, перпендикулярной к плоскости проекции, является частным случаем параллельного перемещения.
Отличие от общего случая состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.
Вращение точки вокруг оси 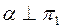 , иллюстрирует рис. 8а. Точка В перемещается в новое положение В1 по окружности, принадлежащей проекции плоскости
, иллюстрирует рис. 8а. Точка В перемещается в новое положение В1 по окружности, принадлежащей проекции плоскости 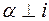 . Так как
. Так как 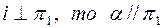 . Поэтому при вращении точки вокруг оси, перпендикулярной к горизонтальной плоскости проекции, ее горизонтальная проекция перемещается по окружности, центр которой принадлежит горизонтальной проекции оси вращения, а фронтальная проекция точки — по прямой, параллельной оси х (рис. 8,6).
. Поэтому при вращении точки вокруг оси, перпендикулярной к горизонтальной плоскости проекции, ее горизонтальная проекция перемещается по окружности, центр которой принадлежит горизонтальной проекции оси вращения, а фронтальная проекция точки — по прямой, параллельной оси х (рис. 8,6).
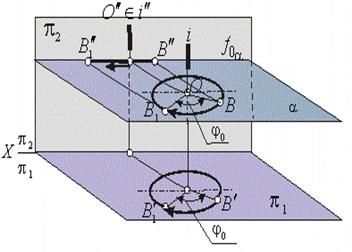 | 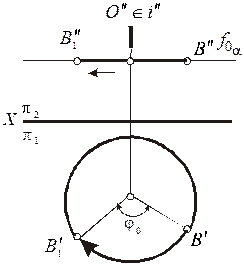 | ||
Рис.8,а Рис.8,б
Если проследить, как будет изменяться положение точки А при ее вращении вокруг оси i, перпендикулярной плоскости 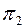 . То точка А будет перемещаться по дуге окружности в плоскости
. То точка А будет перемещаться по дуге окружности в плоскости  и, следовательно,
и, следовательно, 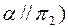 , поэтому эта окружность проецируется на плоскость
, поэтому эта окружность проецируется на плоскость 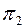 без искажения, а на плоскость
без искажения, а на плоскость 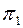 — в отрезок прямой, параллельной оси х . Таким образом, при вращении точки вокруг оси, перпендикулярной к фронтальной плоскости проекции, фронтальная проекция точки перемещается по окружности с центром на фронтальной проекции оси вращения, а горизонтальная — по прямой, параллельной оси х. Выяснив характер проекций траекторий перемещения точки при ее вращении вокруг оси, перпендикулярной плоскости проекции, легко осуществить перемещение любой геометрической фигуры из заданного положения в частное путем ее поворота вокруг оси
— в отрезок прямой, параллельной оси х . Таким образом, при вращении точки вокруг оси, перпендикулярной к фронтальной плоскости проекции, фронтальная проекция точки перемещается по окружности с центром на фронтальной проекции оси вращения, а горизонтальная — по прямой, параллельной оси х. Выяснив характер проекций траекторий перемещения точки при ее вращении вокруг оси, перпендикулярной плоскости проекции, легко осуществить перемещение любой геометрической фигуры из заданного положения в частное путем ее поворота вокруг оси  . В качестве примера покажем на эпюре Монжа, как осуществляется перемещение отрезка произвольной прямой в частное положение путем вращения вокруг оси, перпендикулярной плоскости проекции.
. В качестве примера покажем на эпюре Монжа, как осуществляется перемещение отрезка произвольной прямой в частное положение путем вращения вокруг оси, перпендикулярной плоскости проекции.
ПРИМЕР 1. [CD] прямой общего положения b перевести в положение 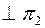 (рис.9).
(рис.9).
Чтобы осуществить перемещение отрезка из общего положения в проецирующее, необходимо последовательно выполнить два вращения вокруг осей, перпендикулярных к плоскостям проекций.
После первого вращения отрезок переводится в положение, параллельное плоскости 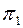 (или
(или 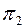 )-задача 1, и лишь после этого вращением вокруг оси, перпендикулярной плоскости проекции
)-задача 1, и лишь после этого вращением вокруг оси, перпендикулярной плоскости проекции 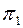 (или
(или 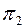 ) перемещают отрезок в положение, перпендикулярное плоскости
) перемещают отрезок в положение, перпендикулярное плоскости 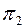 (или
(или 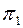 )-задача 2.
)-задача 2.
Для упрощения геометрических построений ось вращения следует выбирать так, чтобы она пересекала вращаемую прямую.
Дата добавления: 2016-04-14; просмотров: 647;
