Линза между свечой и экраном

Автор: Рассмотрим такую ситуацию. Небольшой предмет (например, горящая свеча) и экран закреплены неподвижно на некотором расстоянии друг от друга. Между ними находится собирающая линза, которую можно передвигать от свечи к экрану и обратно (рис. 8.27). При определенном положении линзы на экране получается четкое изображение свечи (как мы уже знаем, это действительное перевернутое изображение). Пусть при этом линейное увеличение предмета составляет величину k₁ (которая может быть как больше, так и меньше единицы). Нам необходимо определить: 1) существует ли еще одно положение линзы, при котором на экране получается четкое изображение предмета; 2) если такое положение существует, то каким будет линейное увеличение k₂ в этом случае.

Рис. 8.27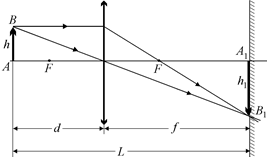

Читатель: По-моему, тут можно воспользоваться принципом обратимости световых лучей. То есть если пустить лучи на рис. 8.27 в обратную сторону, то стрелка А₁В₁ станет предметом, а предмет АВ – ее изображением. А это значит, что если расположить линзу на расстоянии f от предмета, то изображение получится за линзой на расстоянии d. При этом ясно, что если сначала линейное увеличение было 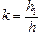, то теперь оно равно .

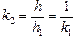Автор: Вы правы. А полученную Вами формулу следует запомнить:

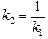. (8.9)

Поставим еще один вопрос: на какое расстояние l надо сместить линзу из первого положения, при котором она дает четкое изображение предмета на экране, чтобы она оказалась во втором положении, при котором она опять дает четкое изображение на экране? Будем считать, что величины d и f – расстояния от предмета до линзы и от линзы до экрана в первом положении известны.

Читатель: Сначала «развернем» на 180° рис. 8.27, предварительно развернув его лучи в обратную сторону. Тогда предмет А₁В₁ будет находиться от луча на расстоянии f, а изображение АВ – на расстоянии d (рис. 8.28).

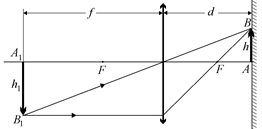Рис. 8.28

Теперь мы вполне можем заменить перевернутую стрелку А₁В₁ обычной стрелкой АВ, такой же, как на рис. 8.27. Изображение этой стрелки также получится на экране четким. Это следует из формулы линзы: если линза та же и расстояние от линзы до предмета такое же, то и изображение должно остаться на том же самом месте (рис. 8.29).

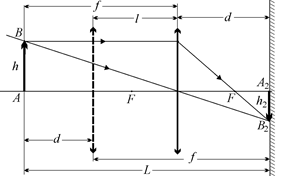Рис. 8.29

Из рис. 8.29 легко видеть, что новое положение линзы смещено относительно старого положения на расстояние

l = f – d. (8.10)

Автор: Совершенно верно.

СТОП! Решите самостоятельно: В27, В28, С18, С19.

Автор: Рассмотрим такой вопрос: всегда ли, разместив линзу между предметом и экраном (см. рис. 8.27), мы сможем найти два таких положения, при которых на экране получится четкое изображение предмета?

Читатель: Я думаю – нет. Если линза очень «слабая», то при малом расстоянии между предметом и экраном она «не сумеет» собрать лучи на экране так, чтобы получилось четкое изображение.

Автор: Вы правы. Убедимся в этом чисто алгебраически.

Пусть расстояние от линзы до экрана L, расстояние от предмета до линзы d, а фокусное расстояние линзы F. Тогда справедлива формула линзы

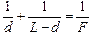(1)

(здесь учтено, что расстояние от линзы до экрана f = L – d). Попробуем решить это уравнение относительно d:

,

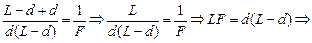
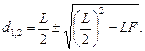
Ясно, что решения возможны, только если

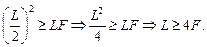
Если L < 4F, то получить четкое изображение предмета не удастся ни при каком положении линзы. Если L = 4F, то получится четкое изображение предмета только при одном положении линзы: при d = L/2. Это как раз тот случай, когда предмет находится от линзы на двойном фокусном расстоянии, и его изображение получается за линзой также на двойном фокусном расстоянии. При этом линейное увеличение k = 1.

Итак, для того чтобы можно было получить четкое изображение предмета с помощью собирающей линзы с фокусным расстоянием F, расстояние от предмета до экрана должно удовлетворять условию

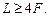(8.11)

СТОП! Решите самостоятельно: В29, В30, С5, С20, С21.