Воздушная полость в стекле
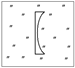Рис. 8.9
|
Воздушная полость в стекле имеет форму плоско-вогнутой линзы (рис. 8.9). Найти фокусное расстояние F1 этой линзы в стекле. Известно, что линза, изготовленная из этого же стекла и совпадающая по форме с полостью, имеет в воздухе фокусное расстояние F. Показатель преломления стекла равен п. Углы между падающими и преломленными лучами считать малыми.
| п F | Решение. Заметим, что в данном случае «материал», из которого «изготовлена» линза – это воздух, а его абсолютный показатель преломления плинзы = 1. «Средой» же является стекло с абсолютным показателем преломления псреды = п. Тогда формула (8.1) для данной воздушной линзы будет иметь вид |
| F1 = ? | |
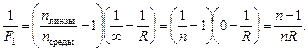
Отсюда
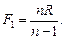(1)
Для такой же по форме и размерам стеклянной линзы справедливо
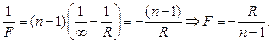(2)
Выразим R из (2) и подставим в (1), получим
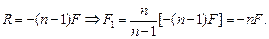
Знак «минус» показывает, что если стеклянная линза – рассеивающая (F < 0), то «воздушная» – собирающая (F1 > 0).
Ответ: F1 = –nF.
СТОП! Решите самостоятельно: В4, С2, С3.
Собирающая линза
Действительное изображение. Возьмем собирающую линзу с фокусным расстоянием F. На расстоянии d перед плоскостью линзы поместим небольшой предмет, расположенный параллельно плоскости линзы (отрезок АВ, рис. 8.10).
Найдем расстояние f от плоскости линзы до изображения предмета (отрезок А¢В¢). Как видно из рис. 8.10, главный задний фокус линзы находится в точке F2, а передний – в точке F1.
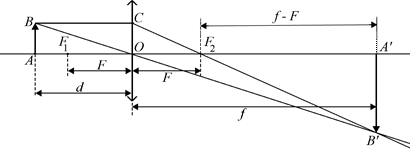
Рис. 8.10
1. Рассмотрим подобные треугольники АОВ и А¢ОВ¢. Поскольку DАОВ ∾ DА¢ОВ¢, то
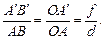(1)
2. Рассмотрим подобные треугольники CF2O и А¢F2В¢. Поскольку D CF2O ∾ DА¢F2В¢, то
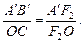(2)
Поскольку ОС = АВ, F2O = F и А¢F2 = f – F, равенство (2) можно записать в виде
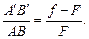(3)
Приравнивая правые части равенств (1) и (3), получим:
.
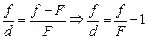Разделим обе части последнего равенства на f и получим
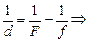
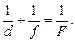(8.3)
Равенство (8.3) называется формулой линзы. Эта формула связывает между собой три величины: d, f и F. После того как формула получена, найти величину f не составляет труда:
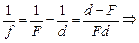
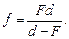(8.4)
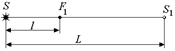Рис. 8.11
|
Задача 8.4. На рис. 8.11 изображены точечный источник света S, его изображение S1, полученное с помощью собирающей линзы, и передний фокус линзы F1. Известны расстояния SF1 = l и SS1 = L. Определить фокусное расстояние линзы.
| SF1 = l SS1 = L | Решение. В данном случае изображение действительное, поэтому источник находится перед передним фокусом линзы (рис. 8.12). Поэтому фокусное расстояние линзы F = d – l, а расстояние от изображения до линзы f = L – d. |
| F = ? | |
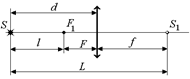Рис. 8.12
|
Применим формулу линзы:
,
.
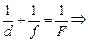
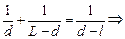
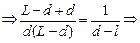
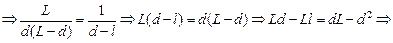
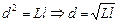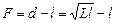Ответ: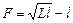 
.
СТОП! Решите самостоятельно: А8, В5, С4.
Дата добавления: 2016-04-11; просмотров: 1788;