Всегда ли двояковыпуклая линза собирающая?

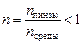Если линза двояковыпуклая, то R₁ > 0 и R₂ > 0. У рассеивающей линзы D < 0. Выражение в этом случае может быть отрицательным, только если(п – 1) < 0, то есть или п_л < п_ср. Следовательно, если мы подберем для линзы такой проз­рачный материал, чтобы его абсолютный показатель преломления п_л был меньше абсолютного показателя преломления среды п_ср, в которой эта линза будет находиться, то в таком случае двояковыпуклая линза будет рассеивающей.

Задача 8.2. Двояковыпуклая линза, сделанная из стекла с показателем преломления п = 1,6, имеет фокусное расстояние F = 10 см. Чему будет равно фокусное расстояние этой линзы, если ее поместить в прозрачную среду, имеющую показатель преломления п₁ = 1,5? Найти фокусное расстояние этой линзы в среде с показателем преломления п₂ = 1,7.

F = 10 см, п = 1,6 п1 = 1,5, п2 = 1,7	Решение. Так как в пустоте фокусное расстояние равно F, то согласно формуле (8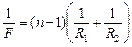.1) . (1)
F = ?

В среде с абсолютным показателем преломления п_среды относительный показатель преломления стекла будет равен 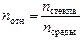. Тогда для фокусных расстояний F₁ и F₂ можем записать:

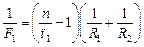, (2)

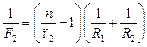, (3)

Из уравнения (1) выразим 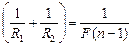и подставим в уравнение (2), получим

.

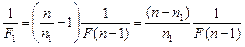Отсюда

.

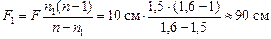Аналогично, подставляя 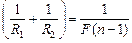в уравнение (3), получила

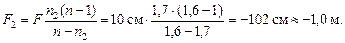
Ответ: F₁ » 90 см, F₂ » –1,0 м.

СТОП! Решите самостоятельно: А5–А7, В2, В3.

Бессильная» линза

Читатель: А какую оптическую силу будет иметь стеклянная выпукло-вогну­тая линза, у которой радиусы сферических поверхностей равны |R₁| = |R₂| = R (рис. 8.7)?

Автор: В этом случае R₁ = +R, а R₂ = –R. Тогда согласно формуле (8.2) оптическая сила линзы равна:

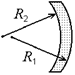Рис. 8.7

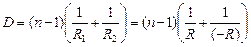=0.

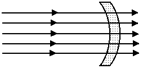Рис. 8.8

А раз оптическая сила равна нулю, то главное фокусное расстояние рав­но , то есть F стремится к бесконечности. Это значит, что после прохождения такой линзы пучок параллельных лучей остается параллельным. То есть линза НИКАК не изменяет ход лучей. По здравому смыслу это и понятно: раз оптическая сила линзы равна нулю, значит, линза БЕССИЛЬНА как-то влиять на ход лучей (рис. 8.8).

Заметим, что именно такую форму иногда придают стеклянным оправам ручных часов.