Фокусное расстояние линзы

Читатель: В предыдущем параграфе мы выяснили, что если на собирающую линзу направить пучок лучей, параллельных главной оптической оси, то после преломления все лучи пересекутся в одной точке, называемой главным фокусом линзы. Возникает вопрос: а почему все эти лучи после преломления пересекутся в одной точке? То есть нельзя ли доказать (исходя из закона преломления света), что все параллельные лучи после преломления на двух сферических поверхностях линзы действительно пересекутся в одной точке?

Автор: Это можно доказать, но с двумя существенными оговорками: 1) лучи мы будем рассматривать только параксиальные, то есть идущие на малых расстояниях от главной оптической оси линзы; 2) линзу будем считать тонкой, то есть толщиной линзы мы будем пренебрегать по сравнению с фокусным расстоянием линзы. Дело в том, что, строго говоря, параллельные лучи после преломления в собирающей линзе в одной точке не пересекаются. Но с учетом сделанных допущений можно попробовать провести доказательство чисто теоретически.

Рассмотрим луч РМ, падающий на линзу параллельно ее главной оптической оси. Пусть этот луч встречает первую преломляющую поверхность линзы в точке М на высоте h над осью, причем h гораздо меньше, чем С₂О и С₁О (рис. 8.1).

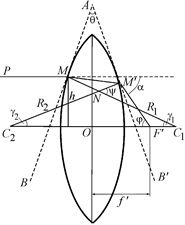Рис. 8.1

Преломленный луч пойдет по направлению ММ' и, преломившись снова на второй ограничивающей линзу поверхности, выйдет излинзы по направлению M'F', составляющем с главной оптической осью угол j. Точку пересечения этого луча с главной оптической осью обозначим через F', а расстояние от этой точки до оптического центра линзы – через f '.

Проведем через точки M и М' плоскости, касательные к преломляющим поверхностям линзы. Эти касатель­ные плоскости (перпендикулярные к плоскости чертежа) пересекутся под некоторым углом q, причем угол q весьма мал, так как рассматриваемая нами линза – тонкая.

Заметим, что поскольку угол преломления луча зависит только от угла падения и показателя преломления материала линзы относительно среды, то мы можем заменить сферическую поверхность с центром в точке С₁ на плоскость АВ, которая касается этой сферической поверхности в точке М. Угол преломления луча РМ при этом не изменится.

Точно так же преломление луча ММ¢ на сферической поверхности с центром в точке С₂ мы можем заменить на преломление этого луча на плоскости АВ¢, которая касается сферической поверхности в точке М¢. То есть луч РМ преломится в линзе так, как если бы он проходил через тонкую призму ВАВ¢, образованную проведенными нами в точках М и М¢ касательными плоскостями АВ и АВ¢.

В § 6 мы доказали, что при преломлении в тонкой призме с малым преломляющим углом q луч отклоняется от первоначального направления на угол a = (п – 1)q (формула (6.3)), где п – показатель преломления вещества, из которого сделана призма. В нашем случае (см. рис. 8.1) угол отклонения луча от первоначального направления – это угол j, то есть

j = (п – 1)q. (1)

Пусть С₁ и С₂ – центры сферических преломляющих поверхностей линзы, а R₁ и R₂ – соответственно радиусы этих поверхностей. Радиус С₁М перпендикулярен к касательной плоскости АВ, а радиус С₂М¢ – к касательной плоскости АВ¢.

Как мы знаем из геометрии, углы со взаимно перпендикулярными сторонами равны, поэтому ÐС₁NM¢ – угол между перпендикулярами к касательным плоскостям АВ и АВ¢, который мы на рис. 8.1 обозначим буквой y, равен углу между самими касательными АВ и АВ¢, т.е. углу q:

y = q. (2)

С другой стороны, угол y, как внешний угол в треугольнике С₁NС₂, равен сумме углов g₁ и g₂, образуемых радиусами R₁ и R₂ с осью С₁С₂:

y = g₁ + g₂. (3)

Подставляя (3) в (2), а (2) в (1), получаем

j = (п – 1)(g₁ + g₂). (4)

Мы предположили, что расстояние h мало по сравнению с радиу­сами сферических поверхностей R₁и R₂и с расстоянием f ' точки F' от оптического центра линзы. Поэтому углы g₁, g₂и j также малы, и мы можем заменить синусы этих углов самими углами. Далее, благодаря тому, что линза тонкая, мы можем пренебречь ее толщиной, считая C₁О = R₁; С₂О = R₂, а также пренебречь разницей в высоте точек М и М', считая, что они расположены на одной и той же высоте h над осью. Таким образом, мы можем приближенно считать, что

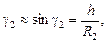
(5)

Подставляя эти равенства в формулу (4), получим

(6)

или, сокращая на h,

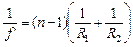, (7)

отсюда

(8)

Весьма существенно, что h не входит в окончательный результат. Это означает, что любой луч, параллельный главной оптической оси линзы, встре­чающий линзу на любом, но достаточно малом по сравнению с R₁ и R₂ расстоянии h от оси, пройдет после пре­ломления в линзе через одну и ту же точку F', лежащую на расстоянии f ' от оптического центра линзы.

В дальнейшем фокусное расстояние мы будем обозначать буквой F, тогда формула (7) будет иметь вид

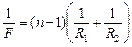. (8.1)

Таким образом, доказано, что линза имеет главный фокус, и формула (8.1)показывает, как фокусное расстояние зависит от показателя преломления вещества, из которого сделана линза, и от радиусов кри­визны ее преломляющих поверхностей.

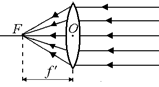Рис. 8.2

Читатель: Мы рассматривали пучок параллельных лучей, идущий слева направо. То есть мы определили, на каком расстоянии от плоскости линзы находится ее задний главный фокус. А как нам найти положение переднего главного фокуса? Ведь, вообще говоря, неочевидно, что он будет находиться на таком же расстоянии от плоскости линзы, что и задний.

Автор: Давайте направим на линзу пучок параллельных лучей, идущих в обратном направлении, то есть справа налево (рис. 8.2). При этом изменится только порядок, в котором падающие на линзу лучи будут преломляться на сферических поверхностях.

Если в формуле (8.1) заменить R₁ на R₂, а R₂ на R₁, то величина F от этого не изменится! А значит, передний фокус симметричен заднему фокусу относительно плоскости линзы (разумеется, при условии, что слева и справа от линзы одна и та же среда).