Мнимое изображение.

Читатель: А какой будет формула линзы, если источник поместить между передним фокусом и плоскостью линзы? Ведь, как мы знаем из § 7, в этом случае собирающая линза дает мнимое изображение.

Автор: Указанный Вами случай показан на рис. 8.13.

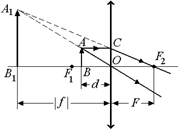Рис. 8.13

Договоримся, что расстояние f от изображения до линзы мы будем брать со знаком «плюс», если изображение действительное, и со знаком «минус», если изображение мнимое (так как действительное изображение находится ЗА линзой, а мнимое – ПЕРЕД ней).

В нашем случае изображение как раз мнимое, поэтому величина f отрицательная, и ОВ₁ = |f|.

Теперь рассмотрим подобные треугольники:

DОАВ ∾ DОА₁В₁ Þ

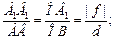(1)

D А₁В₁F₂ ∾ DСОF₂ Þ

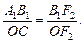
С учетом того, что ОС = АВ, OF₂ = F и B₁F₂ = |f| + F, последнее равенство можно переписать в виде

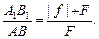(2)

Приравнивая правые части равенств (1) и (2), получим

.

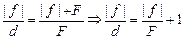Разделим левую и правую части равенства на | f |, получим

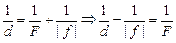. (3)

Поскольку f < 0, то | f | = –f, тогда равенство (3) примет вид

. (4)

Как видим, с учетом того, что f < 0, формула линзы для случая мнимого изображения имеет такой же вид, как и для случая действительного изображения (см. формулу (8.3)).

Задача 8.5. Изображение предмета в собирающей линзе находится на расстоянии 6 см перед плоскостью линзы, а сам предмет – на расстоянии 5 см перед плоскостью линзы. Определите фокусное расстояние линзы. Значения считать точными.

Решение. Поскольку и предмет, и изображение находятся по одну сторону от линзы, значит, изображение мнимое (см. рис. 8.13). Тогда d = 5 см, а f = –6 см. Воспользуемся формулой линзы:

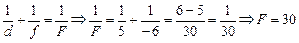см.

Ответ: F = 30 см.

СТОП! Решите самостоятельно: А9, А10, В6, В10, С6.

Мнимый источник.Рассмотрим такую ситуацию: на собирающую линзу падает сходящийся пучок лучей (рис. 8.14).

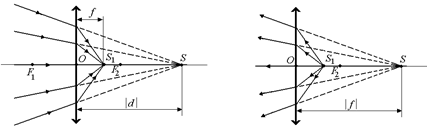
а б

Рис. 8.14

Этот пучок собрался бы в одну точку, если бы линзы на его пути не было. В этом случае точку пересечения продолжений лучей, падающих на линзу – точку S – называют мнимым источником.

Выведем формулу линзы для этого случая. Договоримся, что величина d – расстояние от источника до линзы берется со знаком «плюс», если источник действительный, и со знаком «минус», если источник мнимый (так как действительный источник всегда находится перед линзой, а мнимый – за ней).

В нашем случае d < 0 (рис. 8.14, а), а точка S расположена на расстоянии |d| от плоскости линзы. Заметим, что величина f > 0, поскольку изображение действительное: после преломления в линзе лучи пересекаются в одной точке S₁, образуя тем самым действительное изображение мнимого источника.

Чтобы вывести формулу линзы для данного случая, воспользуемся принципом обратимости световых лучей, то есть мысленно пустим лучи в обратном направлении. Тогда получится, что в точке S₁ находится действительный источник света, и лучи, исходящие из этого источника, преломляются в линзе так, что их продолжения пересекаются в точке S, образуя мнимое изображение (рис. 8.14, б). Таким образом, мы пришли к только что разобранному нами случаю, когда собирающая линза дает мнимое изображение. Формула линзы в этом случае имеет вид

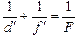, (1)

где d¢ = OS₁ > 0, а f¢ = –OS < 0. Подставляя значения d¢ и f¢ в (1), получим

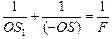. (2)

А теперь вернемся к нашей задаче с мнимым источником (рис. 8.14, а). У нас OS₁ = f > 0, OS = |d| = –d > 0 (d < 0). Подставляя значения OS и OS₁ в формулу (2), получим уже знакомую нам формулу линзы:

,

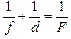только здесь d < 0, а f > 0 и F > 0.

Задача 8.6. На пути сходящегося пучка лучей поставили собирающую линзу с фокусным расстоянием F = 7,00 см. В результате лучи сошлись в точке А на расстоянии f = 5,00 см от линзы. На каком расстоянии b от точки А сойдутся лучи, если линзу убрать?

Из рис. 8.15 видно, что b = |d| – f (величина d < 0, поскольку источник мнимый). Запишем формулу линзы:

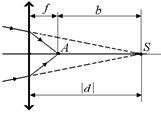Рис. 8.15

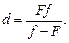
Вычислим искомое расстояние между точками А и S:

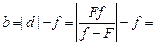
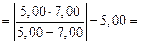
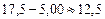см.

Ответ: 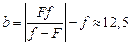см.

СТОП! Решите самостоятельно: А11, В9.

Рассеивающая линза

Действительный источник. Построим изображение предмета в рассеивающей линзе. На рис. 8.16 АВ – это предмет, А₁В₁ – его мнимое изображение, ОВ = d, ОВ₁ = | f | (f < 0, так как изображение мнимое), OF₁ = OF₂ = |F| (фокусное расстояние для рассеивающей линзы F < 0).

Рис. 8.16

Рассмотрим подобные треугольники:

DОАВ ∾ DОА₁В₁ Þ

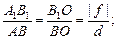(1)

D F₁А₁В₁ ∾ DF₁СО Þ

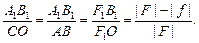(2)

Приравнивая правые части равенств (1) и (2), получим

.

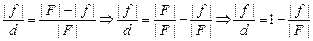Разделим обе части последнего равенства на | f |, получим

.

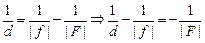Учитывая, что | f | = –f и |F| = –F, получим формулу рассеивающей линзы:

.

Как видим, для рассеивающей линзы по форме записи она ничем не отличается от формулы собирающей линзы (8.3), если правильно учитывать знаки d, f и F. Еще раз напомним, что в данном случае:

d > 0, так как источник действительный,

f < 0, так как изображение мнимое,

F < 0, так как линза рассеивающая.

Задача 8.7. Мнимое изображение светящейся точки в рассеивающей линзе с оптической силой D = –5 дптр находится в два раза ближе к линзе, чем сама точка. Найти положение светящейся точки, если она лежит на главной оптической оси.

D = –5 дптр | f | = d/2	Решение. В нашем случае d > 0, а f < 0, поэтому формулу линзы можно записать в виде 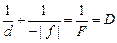, где D < 0.
d = ?

Выразим из этого уравнения d, учитывая, что по условию задачи | f | = d/2:

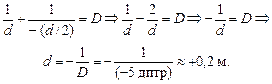
Ответ: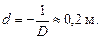

СТОП! Решите самостоятельно: А12, А13, В11.

Мнимый источник.Выведем формулу линзы для случая, когда на рассеивающую линзу падает сходящийся пучок лучей (рис. 8.17).

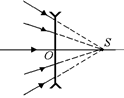Рис. 8.17

Сформулируем задачу более четко: на рассеивающую линзу с известным фокусным расстоянием F < 0 падает сходящийся пучок лучей. Продолжения падающих лучей пересеклись бы за плоскостью линзы на расстоянии OS от нее, если бы линзы на их пути не было. То есть в точке S находится мнимый источник (d = –OS). Найдем величину f – расстояние от плоскости линзы до изображения (действительного или мнимого).

Воспользуемся принципом обратимости световых лучей и мысленно пустим лучи в обратном направлении (рис. 8.18).

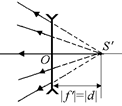Рис. 8.18

Мы получили уже знакомую нам ситуацию: рассеивающая линза дает мнимое изображение в точке S¢ на расстоянии | f ¢| = |d| от плоскости линзы. Требуется найти расстояние d¢ от линзы до источника. Воспользуемся формулой рассеивающей линзы:

, (1)

где f ¢ < 0 и F < 0. Из формулы (1) определим d¢:

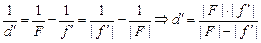. (2)

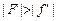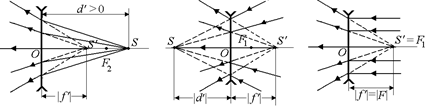
Из формулы (2) следует, что если , то d¢ > 0, значит, источник действительный (рис. 8.19, а), а если 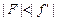, то d¢ < 0, значит, источник мнимый. То есть на линзу падает сходящийся пучок лучей (рис. 8.19, б).

а б в

Рис. 8.19

Если же 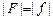, то это значит, что изображение находится в фокусе линзы. В этом случае d ® ¥, то есть на линзу падает параллельный пучок лучей (рис. 8.19, в).

Теперь вернемся к нашей задаче. Поменяем направление лучей на рис 8.19, а и б на обратное и получим графическое решение задачи (рис. 8.20). При этом изображение станет источником, а источник – изображением.

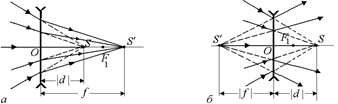
Рис. 8.20

Заменив в формуле (1) d¢ на f, а f ¢ на d, получим формулу линзы для данного случая:

.

Величину f можно легко выразить из формулы линзы

.

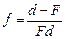Напомним, что здесь d < 0 и F < 0.

Задача 8.8. Сходящийся пучок лучей падает на рассеивающую линзу таким образом, что продолжения всех лучей пересекаются в точке, лежащей на оптической оси линзы на расстоянии b = 15 см от нее. Найти фокусное расстояние линзы в двух случаях:

1) после преломления в линзе лучи собираются в точке, находящейся на расстоянии а₁ = 60 см от линзы;

2) продолжения преломленных лучей пересекаются в точке, находящейся перед линзой на расстоянии а₂ = 60 см от нее.

b = 15 см а1 = 60 см а2 = 60 см	Решение. В первом случае (рис. 8.21) d = –b, f = a1. По формуле линзы имеем
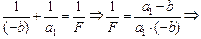
F = ?

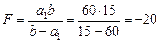см.

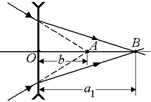
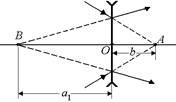
Рис. 8.21 Рис. 8.22

Во втором случае (рис. 8.22) d = –b, f = –a₁. По формуле линзы имеем

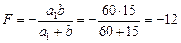см.

Ответ: 1) F = –20 см; 2) F = –12 см.

СТОП! Решите самостоятельно: А14, В12, В13, С7.