Оптическая сила линзы. Какая линза сильнее?

Автор: На рис. 8.3 изображены две собирающие линзы. На каждую из них падает параллельный пучок лучей, который после преломления собирается в главном фокусе линзы. Как Вы считаете (исходя из здравого смысла), какая из двух линз сильнее?

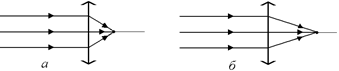
Рис. 8.3

Читатель: По здравому смыслу сильнее линза на рис. 8.3, а, ведь она сильнее преломляет лучи, и поэтому после преломления они собираются ближе к линзе, чем в случае, показанном на рис. 8.3, б.

Автор: Логично. Получается, что чем меньше фокусное расстоя­ние линзы, тем она сильнее. Поэтому для того, чтобы охарактеризо­вать "силу" линзы, физики ввели физическую величину, которую на­зывают оптической силой линзы.

Оптическая сила линзы – это физическая величина, обратная фокусному расстоянию линзы:

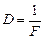. (8.2)

Если фокусное расстояние измеряется в метрах: [F] = м, то [D] = 1/м. Для единицы измерения оптической силы 1/м существует специаль­ное название – диоптрия (дптр).

Итак, оптическая сила линзы измеряется в диоптриях:

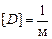= 1 дптр.

Одна диоптрия – это оптическая сила такой линзы, у которой фокусное расстояние равно одному метру: F = 1 м.

Согласно формуле (8.1) оптическая сила собирающей линзы может быть вычислена по формуле

. (8.2а)

Читатель: Мы рассмотрели случай двояковыпуклой линзы, но ведь линзы бывают и двояковогнутые, и вогнуто-выпуклые, и плоско-выпуклые и т.д. Как же вычислять фокусное расстояние линзы в общем случае?

Автор: Можно показать (чисто геометрически), что в любом случае формулы (8.1) и (8.2) будут справедливы, если брать значения радиусов сферических поверхностей R₁ и R₂ с соответствующими знаками: «плюс» – если соответствующая сферическая поверхность выпуклая, и «минус» – если вогнутая.

Например, при расчете по формуле (8.2) оптических сил линз, изображенных на рис. 8.4, следует брать следующие знаки величин R₁ и R₂ в этих случаях: a) R₁ > 0 и R₂ > 0, так как обе поверхности выпуклые; б) R₁ < 0 и R₂ < 0, так как обе поверхности вогнутые; в случае в)R₁ < 0 и R₂ > 0, так как первая поверхность вогнутая, а вторая выпуклая.

Рис. 8.4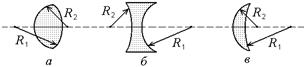

Читатель: А если одна из поверхностей линзы (например, первая) не сферическая, а плоская?

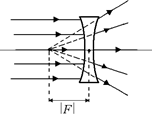Рис. 8.5

Автор: Тогда радиус этой поверхности следует считать равным бесконечности: R₁ ® ¥, тогда .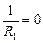

Читатель: Величина F (и, соответственно, D) по формулам (8.1) и (8.2) может получиться отрицательной. Что это значит?

Автор: Это значит, что данная линза рассеивающая. То есть пучок лучей, параллельных главной оптической оси, преломляется так, что сами преломленные лучи образуют расходящийся пучок, но продолжения этих лучей пересекаются перед плоскостью линзы на расстоянии, равном |F| (рис. 8.5).

СТОП! Решите самостоятельно: А2–А4.

Задача 8.1. Преломляющие поверхности линзы являются концентрическими сферическими поверхностями. Большой радиус кривизны R = 20 см, толщина линзы l = 2 см, показатель преломления стекла п = 1,6. Собирающей или рассеивающей будет линза? Найдите фокусное расстояние.

п = 1,6 R = 20 см l = 2 см	Решение. Данная линза является вогнуто-выпуклой (рис. 8.6). Ее первый радиус (с учетом правила знаков) равен R1 = –(R – l) < 0, а второй R2 = R > 0. Согласно формуле (8.1)
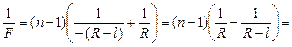
F = ?

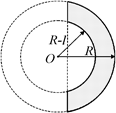Рис. 8.6

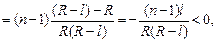
т.е. линза рассеивающая.

Вычислим значение F:

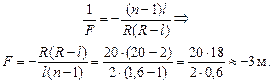
Ответ: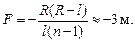

СТОП! Решите самостоятельно: А1, В1, В7, В8, С1.