Дата выдачи и дата погашения ссуды всегда считаются за один день.
При этом возможны два варианта:
- вариант 1: используется точное число дней ссуды и точное число дней в году (365 или 366);
- вариант 2: берётся приблизительное число дней ссуды (продолжительность полного месяца принимается равной 30 дням, а продолжительность года 360 дней). Этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.
Компаундинг.
Простая процентная ставка — это ставка, при которой сумма процента начисляется на первоначально вложенную сумму средств; это означает, что сумма процента, начисленного в предыдущие периоды, не принимается в расчет в процессе последующего наращения.
Для простых процентовиспользуются формулы:
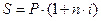 или
или 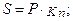 где
где 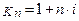 ;
; 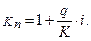
Пример 1.Кредит в размере 10 тыс. руб. выдан 5 августа до 14 ноября под 20% годовых, год високосный. Определить размер наращенной суммы для различных вариантов (обыкновенного и точного) расчета процентов.
Решение. По условию задачи первоначальная сумма ( Р) равна 10 тыс. руб, относительная величина простой процентной ставки (i) составляет0,2.
Наращенную сумму определим по формуле 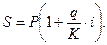
1. В случае точных процентов берем: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 31 день, ноябрь -14 дней. Итого : продолжительность периода начисления процентов составит:
q = 26+30+31+14=101 день.
S = 10 (1 + 101/366 ∙ 0,20) = 10 ∙1,0552 = 10,552 тыс.руб.
2. Для обыкновенных процентов с приближенным числом дней ссуды: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 30 дней, ноябрь -14 дней. Итого : продолжительность периода начисления процентов составит q = 26+30+30+14= 100 дней.
S=10 (1+100/360 ∙ 0,20) = 10 ∙ 1,0556 = 10,556 тыс.руб.
Ответ:наращенная сумма составит: в случае расчёта точных процентов – 10,552 тыс.руб., для обыкновенных процентов с приближённым числом дней – 10,556 тыс. руб.
Пример 2.Кредит в размере 20 тыс.руб. выдается на 2,5 года. Проценты начисляются один раз в конце срока, но ставка процентов за первый год - 30%, а за каждое последующее полугодие она уменьшается на 1%. Определить множитель наращения и наращенную сумму.
Решение. По условию задачи первоначальная сумма (Р) равна 20 тыс.руб.; продолжительность периода начисления процентов в годах (n) составляет 2,5 года; относительные величины простых процентных ставок (i) по периодам начисления составят: за два полугодия первого года - i1= 0,3; за первое полугодие второго года - i2=0,29; за второе полугодие второго года - i3=0,28; за первое полугодие третьего года - i4 =0,27.
1. Используем формулу для определения множителя наращения при различных процентных ставках на разных интервалах
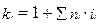 ; кн = 1 + 0,3 + 0,5 (0,29 + 0,28 + 0,27) = 1,72.
; кн = 1 + 0,3 + 0,5 (0,29 + 0,28 + 0,27) = 1,72.
2. Используем формулу для определения наращенной суммы при заданном множителе наращения: S = P x kн .
S = 20 x 1,72 = 34,4 тыс.руб.
Ответ: множитель наращения равен 1,72, а наращенная сумма – 34,4 тыс.руб.
Пример 3.Определить период начисления, за который первоначаль-ный капитал в размере 25000 руб. вырастет до 40000 руб., если используется простая ставка 28 процентов годовых.
Решение. По условию задачи наращенная сумма (S) составляет 40000 руб., а первоначальная (P) - 25000 руб.; относительная величина простой процентной ставки ( i) составит 0,28.
По формуле для определения периода начисления: 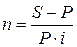 получаем :
получаем : 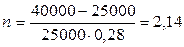 года.
года.
Ответ: период начисления составит 2,14 года, т.е. 2 года и 2 месяца.
Пример 4.Определить простую ставку процентов, при которой первоначальный капитал в размере 24000 руб. достигнет 30000 руб. через год.
Решение: По условию задачи величина первоначальной денежной суммы (P) составляет 24000 руб.; наращенной суммы (S) - 30000 руб., продолжительность периода начисления процентов в годах (n) - 1 год.
По формуле для определения относительной величины простой процентной ставки 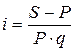 определяем:
определяем: 
Ответ:простая процентная ставка составит 25% годовых.
Сложная процентная ставка— это такая ставка, при которой процент начисляется на постоянно нарастающую базу с учетом процентов, начисленных в предыдущие периоды («проценты на проценты»):
Для сложных процентов 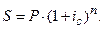
Множитель наращения kн.с. соответственно будет равен
kн.с. = (1 + ic)n.
Если срок ссуды n в годах не является целым числом, множитель наращения определяют по выражению: kн.с. = (1 + ic)nа (1+ nb ic), где
n = nа + nь;
nа – целое число лет;
nь – оставшаяся дробная часть года.
Пример 5.Первоначальная сумма долга (Р) равна 50 тыс.руб. Определить наращенную сумму (S) через 2,5 года по ставке 25% годовых.
Решение
По формуле S = P ( 1 + ic)na (1 + ic nb) получаем
S = 50(1 + 0,25)2 (1 + 0,5∙0,25) = 50∙1,5625∙1,125 =50∙1,7578= 87,89 тыс.руб.
Ответ:наращенная сумма составит 87,89 тыс.руб.
Дата добавления: 2016-04-02; просмотров: 1988;
