Задачи с геометрическими построениями
Задача 8.14. Фокусное расстояние собирающей линзы F = 50 мм. Точечный источник света находится на расстоянии d = 60 мм от линзы на ее главной оптической оси MN. линзу разрезали по диаметру на две равные части, которые раздвинули на расстояние s = = 10 мм симметрично относительно оси MN. определите расстояние Н между двумя изображениями источника света.
| F = 50 мм d = 60 мм s = 10 мм | Решение. Каждая половина линзы действует как целая линза. Пусть А1 и А2 – изображения точки А в верхней и нижней половинках линзы. Рассмотрим лучи АА1 и АА2, проходящие через оптические центры О1 и О2 верхней и нижней поло- |
| Н = ? | |
винок линзы (рис. 8.30). Тогда искомое расстояние Н между изображениями А1 и А2 равно:
Н = А1А2 = А1В1 + В1В2 + В2А2 = h + s + h = 2h + s. (1)
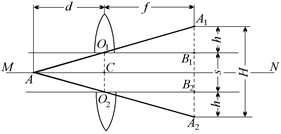Рис. 8.30
Величину h можно найти из подобия DАО1С и DО1А1В1:
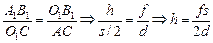. (2)
Осталось определить величину f, которую найдем из формулы линзы: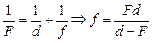 
. Подставив это значение f в (2), получим:
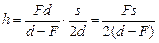. (3)
Найдем Н, подставив (3) в (1):
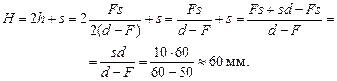
Ответ: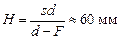 
.
СТОП! Решите самостоятельно: С26, С27, D4–D6.
Пятно на экране
Задача 8.15. На всю поверхность собирающей линзы, имеющей диаметр D и фокусное расстояние F, направлен пучок лучей, параллельных главной оптической оси. На каком расстоянии L от линзы надо поставить экран, чтобы на нем получился светлый круг диаметром d?
| F d D | Решение. Построим ход двух лучей, падающих на края линзы (рис. 8.31). Из рисунка видно, что возможны два положения экрана, при которых на экране получится круг диаметром d: одно перед главным фокусом линзы на расстоянии L1 от нее, а второе за главным фокусом линзы на расстоянии L2 от нее. |
| L = ? | |
Рис. 8.31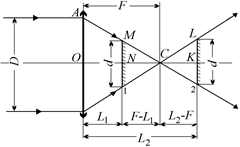 
Величину L1 найдем из подобия DСАО и DСMN:
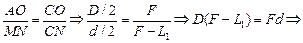
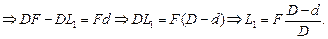
Величину L2 найдем из подобия DСАО и DСLK:
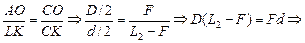
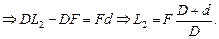
Ответ: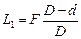 
; 
.
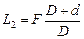СТОП! Решите самостоятельно: В33, С28–С30.
Задача 8.16. Собирающая линза с фокусным расстоянием F = = 5,0 см вставлена в круглое отверстие радиуса r = 3,0 см в доске. Точечный источник света находится на главной оптической оси линзы на расстоянии d = 15 см от нее. По другую сторону доски помещен лист бумаги, на котором получается четкое изображение источника. Каков будет радиус R светлого круга на листе бумаги, если линзу вынуть из отверстия?
| F = 5,0 см d = 15 см r = 3,0 см | Решение. Размер пятна на экране определяется крайними лучами SA и SB, исходящими из источника и проходящими через отверстие (рис. 8.32). Искомый радиус пятна R = AS1. |
| R = ? | |
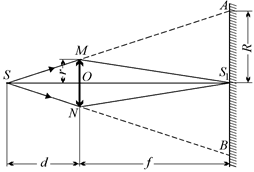Рис. 8.32
Рассмотрим подобные DSОM и DSS1A:
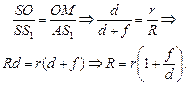(1)
Величину f найдем из формулы линзы:
.
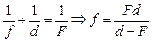Подставим это значение f в (1):
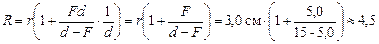см.
Ответ: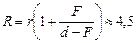 
см.
СТОП! Решите самостоятельно: В34, В35, С31, С32.
Задачи на движение
Задача 8.17. Точка А движется со скоростью υ = 2 см/с (рис. 8.33). С какой скоростью движется изображение, если d = 15 см, а фокусное расстояние линзы F = 10 см?
| υ = 2 см/с d = 15 см F = 10 см |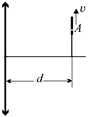 
| Решение. Когда точка А пройдет путь DS, ее изображение (точка А1) пройдет путь DS1 (рис. 8.34), причем 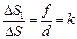 – линейное увеличение отрезка DS.
|
| υ1 = ? | ||
| Рис. 8.33 |
Рис. 8.34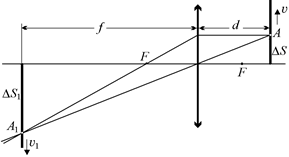 
Отсюда
(мы воспользовались формулой линзы).
Если расстояние DS было пройдено за время Dt, то
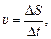(1)
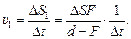(2)
Разделим уравнение (2) на (1), получим
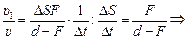
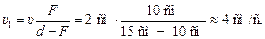
Ответ: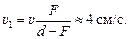 
СТОП! Решите самостоятельно: В36, В37, С33, С34, D8.
Дата добавления: 2016-04-11; просмотров: 8350;