Проекционный аппарат. Фотоаппарат
Диаскоп
Часто при чтении лекций или проведении научных семинаров возникает необходимость показать на экране большому числу слушателей какое-либо изображение, сделанное на прозрачной пленке – диапозитиве. Для этой цели используется специальный прибор – диаскоп. В него вставляют диапозитив, и на экране появляется его сильно увеличенное изображение.
Возникает вопрос: как же "работает" диаскоп?
 Рис. 9.1
Рис. 9.1
|
Главный секрет диаскопа – это собирающая линза. В самом деле, если на очень малом расстоянии от главного переднего фокуса собирающей линзы поместить небольшой предмет, то собирающая линза даст сильно увеличенное изображение этого предмета (рис. 9.1).
Изображение это действительное и перевернутое. Если в том месте, где получилось изображение, поставить непрозрачный экран (желательно белый), то мы увидим на нем четкое изображение предмета.
Читатель: Но нам же не нужно перевернутое изображение! Нам нужно нормальное изображение.
Автор: Эту проблему легко решить. Достаточно вставить диапозитив в диаскоп "вверх ногами". Тогда изображение как раз получится нормальным. А для того чтобы изображение всегда получалось четким, диапозитив можно перемещать вдоль главной оптической оси линзы, подбирая расстояние между линзой и диапозитивом так, чтобы изображение получалось точно в том месте, где находится экран. Это называется наводкой на резкость.
Теперь, когда основная идея устройства нами понята, рассмотрим схему реального диаскопа (рис. 9.2).
Диапозитив 1 помещается перед фокальной плоскостью собирающей линзы 5, которая называется объективом. Источник света 2 освещает диапозитив с помощью системы линз, которая называется конденсором 3. Конденсор нужен для того, чтобы вся поверхность диапозитива 1 была освещена равномерно. За источником света расположено вогнутое зеркало 4, которое возвращает обратно свет, падающий от источника на заднюю стенку диаскопа. Изображение получается на экране 6.
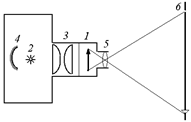 Рис. 9.2
Рис. 9.2
|
Задача 9.1. Какое увеличение k диапозитива дает объектив проекционного фонаря с фокусным расстоянием F = 0,25 м, если экран удален от объектива на расстояние f = 4,0 м?
| F = 0,25 м f = 4,0 м | Решение. Пусть диапозитив находится на расстоянии d от объектива (см. рис. 9.2), тогда можно воспользоваться формулой линзы:
 . (1) . (1)
|
| k = ? | |
Увеличение диапозитива – это линейное увеличение в собирающей линзе:
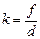 . (2)
. (2)
Выразим d из (2): 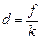 и подставим в (1), получим:
и подставим в (1), получим:
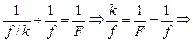
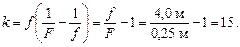
Ответ: 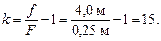
СТОП! Решите самостоятельно: А1, А2, В1, В2.
Фотоаппарат
Я думаю, нет нужды объяснять, что такое фотоаппарат. Но интересно было бы разобраться, как он устроен.
В фотоаппарате есть два основных секрета. Первый секрет – это светочувствительная фотопленка. Если на этой пленке на очень короткое время (доли секунды) удается получить четкое изображение фотографируемого предмета, то это изображение остается на ней навсегда. Дело здесь в химическом (весьма сложном) действии света на фотопленку. В детали химических процессов мы, понятное дело, сейчас вникать не будем.
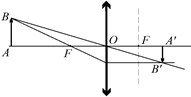 Рис. 9.3
Рис. 9.3
|
Второй секрет – это объектив. В простейшем случае объективом фотоаппарата служит обычная собирающая линза. С ее помощью и удается получать на фотопленке нужные изображения. Принцип действия фотоаппарата показан на рис. 9.3.
Предмет АВ, который мы хотим сфотографировать, обычно находится достаточно далеко от объектива, то есть на расстоянии, значительно превышающем фокусное расстояние объектива. В этом случае изображение получается действительным, перевернутым и сильно уменьшенным. И находится это изображение за задней фокальной плоскостью объектива на очень малом расстоянии от нее. Значит, если в том месте, где находится изображение А¢В¢, поместить фотопленку, то на ней получится четкое изображение предмета АВ.
 Рис. 9.4
Рис. 9.4
|
Теперь рассмотрим схему простейшего фотоаппарата (рис. 9.4). Фотоаппарат состоит из объектива 1 и ящика 2 со светонепроницаемыми стенками. Этот ящик называется камерой. Объектив помещается в передней стенке камеры, а у задней стенки помещают светочувствительную фотопластинку 3. Для получения четкого изображения объектив можно перемещать относительно задней стенки камеры (наводка на резкость).
Промежуток времени, необходимый для освещения фотопластинки (экспозиция) зависит от чувствительности пластинки к свету и от условий освещенности фотографируемого предмета. При фотографировании в яркий солнечный день экспозиция в современных фотоаппаратах составляет сотые и даже тысячные доли секунды. Но если вы захотите тем же фотоаппаратом сфотографировать ночное небо, потребуется экспозиция минут тридцать.
 Рис. 9.5
Рис. 9.5
|
Современные фотоаппараты принципиально устроены точно так же, разница лишь в деталях: например, вместо фотопластинки обычно используется фотопленка, да и размеры у современных фотоаппаратов как правило небольшие (рис. 9.5).
СТОП! Решите самостоятельно: А3, А4, В3, В4.
Задача 9.2. При съемке автомобиля длины l = 4,0 м пленка располагалась от объектива на расстоянии f = 6,0 см. С какого расстояния d снимали автомобиль, если длина его негативного изображения l = 32 мм?
| l = 4,0 м f = 6,0 cм l = 32 мм | Решение. Начертим схему к задаче (рис. 9.6), где АВ – автомобиль, а А¢В¢ – его действительное изображение. Из подобия DАОВ и DА¢ОВ¢ следует | |
| d = ? | ||
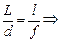
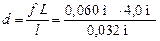 » 7,5 м.
Ответ: » 7,5 м.
Ответ: 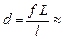 7,5 м. 7,5 м.
|  Рис. 9.6 Рис. 9.6
| |
СТОП! Решите самостоятельно: А5, В4.
Задача 9.3. Определить оптическую силу объектива фотоаппарата, которым фотографируют местность с самолета на высоте 5 км в масштабе 1 : 20 000. В каком масштабе получится снимок, если этим фотоаппаратом сделать съемку поверхности Земли с искусственного спутника, находящегося на высоте 250 км? (Все значения считать точными.)
| h1 = 5 км M1 = 1:20000 h2 = 250 км | Решение. Если масштаб составляет 1 : 20 000, то это значит, что изображение на фотопленке в 20 000 раз меньше оригинала. Иными словами, линейное поперечное увеличение объектива
 . .
|
| М2 = ? |
То есть масштаб и линейное увеличение – это одна и та же величина. В данном случае высота h – это расстояние от предмета до линзы. Пусть f – расстояние от линзы до изображения (от объектива до фотопленки), а F – фокусное расстояние объектива линзы. Тогда по формуле линзы получим
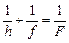 . (1)
. (1)
Теперь учтем, что в условии задачи h >> f, поэтому 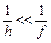 и слагаемым
и слагаемым 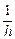 в формуле (1) можно пренебречь. Тогда
в формуле (1) можно пренебречь. Тогда 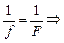 f = F, т.е. изображение получается в фокальной плоскости линзы.
f = F, т.е. изображение получается в фокальной плоскости линзы.
Линейное увеличение k, как известно, равно  . А поскольку линейное увеличение в данном случае равно масштабу, получим формулу
. А поскольку линейное увеличение в данном случае равно масштабу, получим формулу
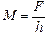 . (9.1)
. (9.1)
Применим эту формулу к нашей задаче. В первом случае
 , (2)
, (2)
во втором случае
 . (3)
. (3)
Разделив уравнение (3) на уравнение (2), получим

 .
.
Ответ: 
СТОП! Решите самостоятельно: А6, А7.
Задача 9.4. С помощью фотоаппарата, имеющего размеры кадра 24´36 мм2 и фокусное расстояние объектива F = 50 мм, проводится фотографирование стоящего человека, рост которого h = 1,8 м. На каком минимальном расстоянии d от человека нужно установить аппарат, чтобы сфотографировать человека во весь рост?
| F = 50 мм h = 1,8 м а´b = 24´36 мм2 | Решение. Ясно, что максимальное изображение человека на пленке имеет размер b = = 36 мм. Тогда линейное увеличение равно
 (1) (1)
|
| d = ? | |
а формула линзы имеет вид
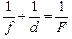 . (2)
. (2)
Выразим f из (1): 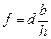 и подставим в (2), получим:
и подставим в (2), получим:


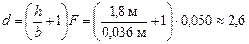 м.
м.
Ответ: 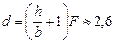 м.
м.
СТОП! Решите самостоятельно: А8, В5–В7, С1, С2.
Задача 9.5. Требуется сфотографировать конькобежца, пробегающего перед фотоаппаратом со скоростью υ = 10 м/с. Определить максимально допустимую экспозицию при условии, что размытость изображения не должна превышать х = 0,2 мм. Главное фокусное расстояние объектива F = 10 см и расстояние от конькобежца до аппарата d = 5 м. В момент фотографирования оптическая ось объектива аппарата перпендикулярна к траектории движения конькобежца.
| υ = 10 м/с х = 0,2 мм F = 10 см d = 5 м | Решение.Экспозицией называется время, в течение которого свет от объекта попадает на фотопленку. Размытость – это расстояние, на которое смещается произвольная точка изображения на фотопленке за то малое время, в течение которого свет попадает на пленку, т.е. за время экспозиции. |
| τ = ? | |
 Рис. 9.7
Рис. 9.7
|
Пусть в начальный момент точка А имела своим изображением точку А¢, а в конечный момент – точку А¢¢ (рис. 9.7). Тогда размытость изображения х = = А¢А¢¢. Отрезок АА1 – это перемещение произвольной точки конькобежца за время экспозиции τ, поэтому АА1 = υτ.
Учитывая, что d >> F, можно приближенно считать, что изображение находится в фокальной плоскости линзы объектива, поэтому f » F. Тогда из подобия DАОА1 и DА¢ОА² можем записать:
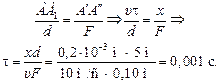
Ответ:  0,001 с.
0,001 с.
СТОП! Решите самостоятельно: В8, С3–С5.
Дата добавления: 2016-04-11; просмотров: 8428;
