Самый простой фотоаппарат – ящик с дыркой

(камера-обскура)

Чтобы сделать фотографию, совершенно необязательно иметь современный цифровой фотоаппарат. Вполне достаточно иметь картонный ящик с маленьким отверстием (диаметром около 0,5 мм) и фотопластинку, которую надо закрепить на задней стенке ящика.

Если поместить перед таким ящиком ярко освещенный предмет, то на задней стенке (там, где находится фотопластинка) мы получим перевернутое изображение предмета (рис. 1.14).

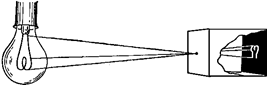Рис. 1.14

Рис. 1.15

Этот результат нетрудно понять. Действительно, от каждой точки источника через отверстие проходит узкий световой пучок, который дает на экране небольшое пятнышко, воспроизводящее форму отверстия. Свет от всего источника в целом дает на экране картину, нарисованную такими светлыми пятнышками, накладывающимися друг на друга. Если размер отверстия таков, что отдельные пятнышки превосходят детали картины, то она получится размытой, плохо передающей объект. Но при достаточно малых размерах отверстия размеры пятнышек будут меньше деталей картины, и изображение получится вполне удовлетворительное.

Рис. 1.15 воспроизводит фотографию, полученную с помощью такой дырочной фотокамеры.

Попробуем ответить на два вопроса:

1) каковы размеры изображения точечного источника света в камере-обскуре?

2) на каком расстоянии друг от друга находятся изображения двух различных точечных источников света в камере-обскуре.

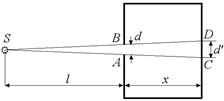Рис. 1.16

На рис. 1.16 показано изображение точки S. Ее изображением является светлое пятно диаметром d¢. Найдем величину d¢, если диаметр «дырки» d, глубина камеры х, а расстояние от источника до дырки l.

Из подобия DSAB и DSDC получим

.

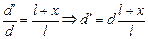То есть размер изображения прямо пропорционален размеру дырки. Ясно, что чем меньше будет d¢ , тем более резким будет изображение. Но! Если величина d¢ будет сравнима с длиной волны ~1 мкм, то уже заметную роль будут играть волновые свойства света, будет происходить дифракция – огибание препятствия – и качество изображения будет ухудшаться.

Теперь попробуем найти расстояние между изображениями двух точечных источников S₁ и S₂ (рис. 1.17).

Рис. 1.17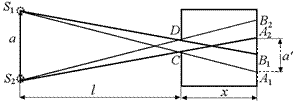

Если расстояние между источниками равно а, то расстояние между изображениями (крайними нижними точками изображений) равно а¢. Рассмотрим подобные треугольники S₁CS₂ и А₁СА₂, тогда из подобия следует

.

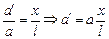Как видим, величина «разрешения», т.е. расстояния от различных точек изображения тем больше, чем больше глубина камеры х.

СТОП! Решите самостоятельно: С13, D2, D3.