Закон отражения света

Падающий луч, отраженный луч и перпендикуляр, восстановленный к отражающей поверхности из точки падения луча, лежат в одной плоскости, причем угол падения равен углу отражения:

a = b. (2.1)

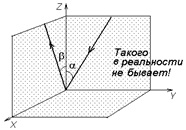Рис. 2.5

Отметим, что для того, чтобы однозначно определить положение отраженного луча, недостаточно просто сказать, что угол падения равен углу отражения. Ведь, вообще говоря, падающий луч, отраженный луч и перпендикуляр, восстановленный к отражающей поверхности из точки падения луча, могут и не лежать в одной плоскости. Например, на рис. 2.5 показана гипотетическая ситуация, когда падающий луч составляет угол a с осью OZ и лежит в плоскости ZOY, а отраженный луч составляет угол b с осью OZ и лежит в плоскости ZOX. При этом угол падения равен углу отражения: a = b. Однако экспериментально установлено, что так, как показано на рис. 2.5, в реальности не бывает.

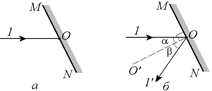
Задача 2.2.На рис. 2.6, а изображен луч 1, падающий на отражающую поверхность MN. Постройте отраженный луч.

Рис. 2.6

Решение.

1. Проведем перпендикуляр к отражающей поверхности: ОО¢^ MN. Падающий луч образует с перпендикуляром ОО¢ некоторый угол a.

2. Проведем луч 1¢ из точки О так, чтобы он составлял с перпендикуляром ОО¢ угол b = a (см. рис 2.6, б).

СТОП! Решите самостоятельно: А1–А3, В1–В3, С1.

Задача 2.3.Под каким углом должен падать луч на плоское
зеркало, чтобы отраженный луч был перпендикулярен падающему?

g = 90°	Решение. Если угол между падающим и отраженным лучами равен 90° (рис. 2.7), то a + b = g = 90°, где a – угол падения, а b – угол отражения. Поскольку согласно закону отражения света	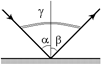Рис. 2.7
a = ?

a = b Þ a + a = g Þ 2a = g Þ a = g/2 = 45°.

Ответ: угол падения a = 45°.

СТОП! Решите самостоятельно: А4–А6, В4.