Как расположить зеркало?
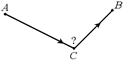 Рис. 2.9
Рис. 2.9
|
Пусть из точки А выходит световой луч (рис. 2.9). Нам нужно, чтобы, отразившись в точке С от зеркала, он попал в точку В. Как должно быть расположено зеркало, чтобы отраженный луч попал в точку В?
Читатель: Если в точке С происходит отражение, значит, угол АСВ – это угол падения a плюс угол отражения b: ÐАСВ = a + b, причем a = b. Построим биссектрису ÐАСВ – луч СD (рис. 2.10, а). Эта биссектриса является перпендикуляром к поверхности зеркала, восстановленным из точки падения луча на зеркало. Теперь осталось только провести отрезок MN^CD – это и есть искомое положение зеркала (рис. 2.10, б).
а 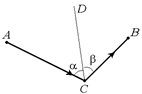 б
б 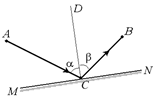
Рис. 2.10
Автор: Совершенно верно.
СТОП! Решите самостоятельно: В7.
Задача 2.5. Человек, идущий по шоссе, увидел в защитном стекле встречного автомобиля Солнце. Под каким углом к горизонту наклонено стекло, если угловая высота Солнца над горизонтом b = 18°, а попадающий в глаз человека отраженный луч направлен горизонтально? Солнце, автомобиль и человек расположены в вертикальной плоскости (рис. 2.11).
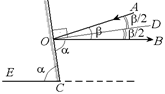 Рис. 2.11
Рис. 2.11
| ||
| b = 18° | Решение. Если OD – нормаль к поверхности стекла, то угол между отраженным лучом и плоскостью стекла ÐВОС = 90° – b/2. (1) | |
| a = ? | ||
Пусть ЕС – горизонтальная линия, ОВ – отраженный луч. Тогда по условию задачи ОВ||ЕС. Тогда ÐВОС = ÐОСЕ = a – как внутренние накрест лежащие углы при параллельных прямых ОВ и ЕС. Отсюда с учетом (1) получим
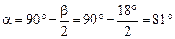 .
.
Ответ: 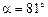 .
.
СТОП! Решите самостоятельно: В8, С3.
Задача 2.6. Узкий луч света, проходя через маленькое отверстие в экране (перпендикулярно к поверхности экрана), попадает на вращающееся шестигранное зеркало, ось вращения которого параллельна поверхности экрана и находится напротив отверстия. Какой длины L будет прочерчивать полоску на экране отраженный от зеркала луч, если расстояние между зеркалом и экраном l = 1,0 м? Размерами граней зеркала по сравнению с расстоянием l пренебречь.
| l = 1,0 м | Решение. В случае, когда грань АВ параллельна экрану (рис. 2.12, а), отраженный луч совпадает с падающим. |
| L = ? | |
а 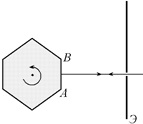 б б 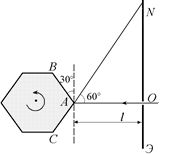
|
Рис. 2.12
Наибольшее отклонение отраженного луча от грани АВ получается тогда, когда зеркало обращено ребром к отверстию (рис. 2.12, б). (При дальнейшем повороте зеркала падающий луч вообще не попадает на грань АВ.)
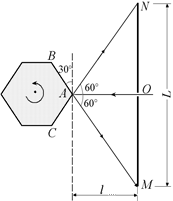 Рис. 2.13
Рис. 2.13
|
Поскольку при повороте зеркала на угол b = 30°, отраженный луч поворачивается на угол 2b = 60° (см. формулу (2.2)), то угол NAO, который составляет отраженный луч AN с гранью АВ, равен 60°. Тогда длина полоски, которую «прочерчивает» отраженный от зеркала луч над точкой О, – это катет ON прямоугольного треугольника AON:
ON = OA×tg60° = ltg60°.
Полоску такой же длины в силу симметрии будет «прочерчивать» луч под точкой О (рис. 2.13). Поэтому общая длина L полоски, которую будет прочерчивать отраженный луч, равна
L = ON + OM = 2ltg60° =
= 2×(1,0 м)×tg60° » 3,5 м.
Ответ: L = 2ltg60° » 3,5 м.
СТОП! Решите самостоятельно: В9, С4, С5.
Изображение в плоском зеркале:
Что это такое?
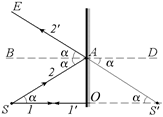 Рис. 2.14
Рис. 2.14
|
Плоское зеркало – это гладкая отражающая поверхность, имеющая форму плоскости.
Пусть рядом с плоским зеркалом находится точечный источник света S (рис. 2.14). Попробуем выяснить, как "ведут себя" отраженные от зеркала световые лучи.
1. Рассмотрим ход луча 1, падающего на зеркало перпендикулярно к его поверхности. Угол падения этого луча a = 0о, следовательно, и угол отражения b = 0о, то есть отраженный луч 1' совпадает с падающим лучом 1. (Пунктиром обозначено продолжение луча 1¢ за плоскость зеркала).
2. Рассмотрим луч 2, падающий на зеркало под некоторым произвольным углом a. Если ВА – перпендикуляр к поверхности зеркала, то отраженный луч 2¢ составляет с перпендикуляром ВА угол a (по закону отражения света).
3. Продолжим пунктиром отраженный луч 2¢ за плоскость зеркала до пересечения с продолжением отраженного луча 1¢ в точке S¢.
4. Попробуем выяснить, что больше: расстояние SO от точечного источника S до плоскости зеркала или S¢O – расстояние от точки пересечения продолжений отраженных лучей 1¢ и 2¢ до плоскости зеркала.
Заметим, что ÐЕАВ = ÐDAS¢ = a (как вертикальные), ÐASO = =ÐВАS = a и ÐDAS¢ = ÐOS'A = a (как внутренние накрест лежащие углы при параллельных прямых BD и SS¢).
Теперь рассмотрим два треугольника: DSАO и DS'AO. Они прямоугольные, имеющие общую сторону АО и равные острые углы (ÐASО = ÐОS¢А = a), следовательно, они равны (по катету и острому углу: DSАО = DS'AO). Отсюда следует:
SO = S¢O.
А это значит, что точки S и S¢ симметричны относительно прямой АО: они лежат на перпендикуляре к прямой АО по разные стороны и на равных расстояниях от нее. Получается, что все лучи, исходящие из точечного источника S и попавшие на зеркало АО отражаются от него так, что продолжения отраженных лучей пересекаются за плоскостью зеркала в одной точке S¢, симметричной точке S.
Читатель: Подождите! Почему Вы говорите, что в точке S¢ пересекаются продолжения всех отраженных от зеркала лучей? Мы ведь рассмотрели только два таких луча: 1 и 2.
Автор: Да, но луч 2 падал на зеркало под совершенно произвольным углом a, и наше доказательство того факта, что SO = S ¢О НИКАК НЕ ЗАВИСЕЛО от величины этого угла. А следовательно, и любой другой луч, исходящий из точки S, отразится от зеркала так, что и его продолжение пройдет через точку S¢. А это значит, что продолжения всех лучей, исходящих из источника S и отраженных от зеркала, пересекутся в одной единственной точке S¢ (рис. 2.15).
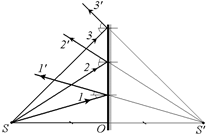 Рис. 2.15
Рис. 2.15
|
Дата добавления: 2016-04-11; просмотров: 2275;
