Метод простой итерации. Итерационными методаминазываются методы последовательных приближений, в которых при вычислении последующего приближения используется предыдущее

Итерационными методаминазываются методы последовательных приближений, в которых при вычислении последующего приближения используется предыдущее, уже известное приближенное решение.

В итерационных методах решение может быть вычислено за бесконечное число итераций (приближений), а поскольку это невозможно, то останавливая процесс вычислений на какой либо итерации, необходимо оценить возникающую при этом погрешность полученного решения.

Рассмосрим метод простой итерации.

Имеем неоднородную СЛАУ, у которой det A ≠0

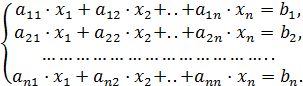(1)

На основании теоремы Кронекера-Капелли СЛАУ (1) имеет единственное решение.

Для применения итерационных методов решения СЛАУ (1)- необходимо его привести к эквивалентному виду:

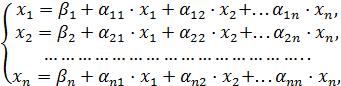(2)

или в векторно-матрчной форме:

,

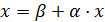где 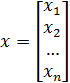; ; 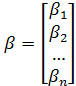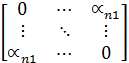. (3)

Приведение к эквивалентному виду может быть выполнено различными способами. Одним из наиболее распространенных является следующий.

а). Разрешим СЛАУ (1) относительно подчеркнутых неизвестных при ненулевых диагональных элементах a_ii≠0, i= .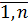

б). Получим следующие выражения для компонентов вектора β и матрицы α эквивалентной системы:

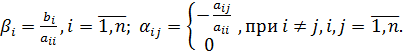(4)

Организуем итерационный процесс:

Нулевое или начальное приближение х⁽⁰⁾ выбирается произвольно, но обычно его принимают равным β, тогда итерационную последовательность векторов вида:

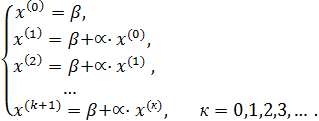(5)

называют методом простой итерации.

Возникает два вопроса:

1. Сходится ли последовательность векторов (5) к единственному решению СЛАУ?

2. Если сходится, то какова возникает ошибка в решении, если остановить итерационный процесс на (к+1)-ой итерации?

Ответ на первый вопрос дают две теоремы.

Теорема1. Достаточным условием сходимости метода простых итераций (5) к единственному решению СЛАУ (1) при любом начальном приближении 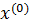является выполнение неравенства

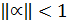(6)

для любой нормы матрицы 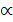эквивалентной системы (3)

Теорема 2.Для сходимости итерационного процесса (5) к единственному решению СЛАУ (1) при любом начальном приближении 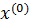необходимо и достаточно, чтобы спектральный радиус матрицы 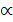был меньше единицы, т.е.

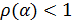, (7)

где 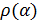- спектральный радиус матрицы .

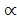Ответ на 2-ой вопрос содержится в утверждении доказанном в работе [1]:

Утверждение: если выполняются условия теоремы (6) или теоремы (7) , то норма погрешности решения 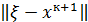возникшей при остановке итерационного процесса на (к+1)-ой итерации будет оцениваться неравенством

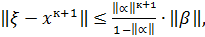(8)

где 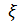- точное решение СЛАУ (1) .

Как правило, при выполнении достаточного условия сходимости итерационного процесса его останавливают при выполнении условия

,

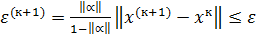где 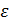- заданная ошибка решения СЛАУ (1).

Метод Зейделя

Метод простых итераций сходится, но иногда недостаточно быстро. Для ускорения существует метод Зейделя, заключающийся в том, что при вычислении элемента 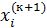вектора неизвестных на (к+1)-ой итерации используется 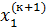, , 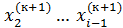уже вычисленные на (к+1)-ой итерации. Значения остальных элементов 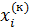, ,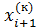…, 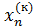берутся из предыдушей итерации х^(к). Так же как и в методе простых итераций строится эквивалентная СЛАУ (2) и за начальное приближение принимается вектор правых частей, т.е. х⁽⁰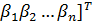⁾=[ . Тогда метод Зейделя для известного вектора предыдущей итерации 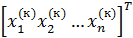на (к+1)-ой итерации будет иметь вид:

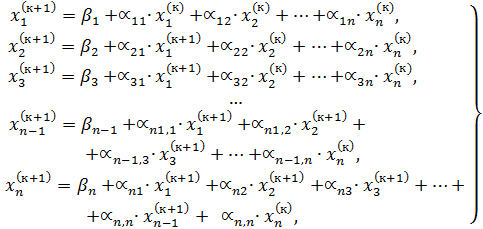(9)

к=0,1,2,3,… .

Из (9) следует, что

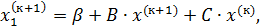(10)

где В – нижняя треугодьная матрица с диагональными элементами равными нулю, так как 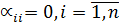; С – верхняя треугольная матрица с диагональными элементами равными нулю, так как .

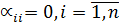Из (10) получаем (Е – В) 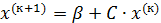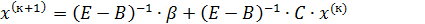, (11)

(11)

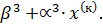
Из(11) следует, что метод Зейделя является методом простой итерации с матрицей правой части 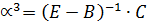и вектором правой части 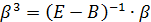. Поэтому условия сходимости по аналогии имеют вид:

(12)

Ошибка решения 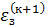, возникающая при остановке итерационного процесса на (К+1)-ой итерации не превышает величины

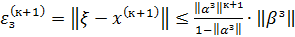, (13)

где к+1 в правой части является показателем степени.

По аналогии с простой итерацией можно записать условие остановки итерационного процесса

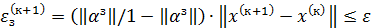- заданная ошибка решения СЛАУ.