Метод скалярной прогонки
Метод прогонки является эффективным методом решения СЛАУ с трехдиагональными матрицами, возникающими при конечно-разностной аппроксимации задач для ОДУ и одномерных уравнений в частных проихводных второго порядка, и является частным случаем метода Гаусса. По экономичности вычислений этот метод имеет существенное преимущество по сравнению с методом Гауса. Рассмотрим каноническую форму СЛАУ
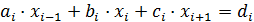 , (*)
, (*)
i= 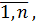
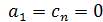 ,
,
где: 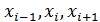 - искомые переменные i-го уравнения;
- искомые переменные i-го уравнения;
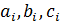 - звдвнные коэффициенты i-го уравнения;
- звдвнные коэффициенты i-го уравнения;
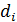 - заданная правая часть i-го уравнения.
- заданная правая часть i-го уравнения.
Представим СЛАУ (*) в обычном виде
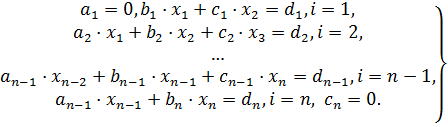 (14)
(14)
Решение СЛАУ или (*) будем искать в виде
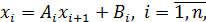 (15)
(15)
где 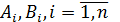 - прогоночные коэффициенты, подлежащие определению.
- прогоночные коэффициенты, подлежащие определению.
Метод скалярной прогонки состоит из двух этапов:
первый этап – прямой ход, где определяются коэффициенты 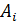 и
и 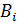 ;
;
второй этап – обратный ход, где определяются искомые параметры в следующей последовательности:
xn→xn-1→xn-2→…→x2→x1.
Получим формулы, определяющие Ai,Bi, i= 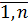 на прямом ходе.
на прямом ходе.
Из первого уравнения в (14)имеем:
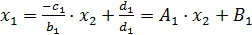 (16)
(16)
откуда 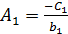 ;
; 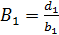 , при i=1.
, при i=1.
Из второго уравнения в (14) с заменой 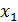 по формуле (16) получаем
по формуле (16) получаем
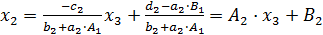 ,
,
где 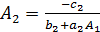 ,
, 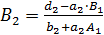 .
.
Продолжая этот процесс, получим из i-го уравнения СЛАУ (14)
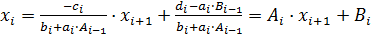 ,
,
при 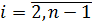 .
.
Следовательно,
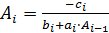 ;
; 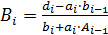 , при
, при 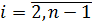 .
.
Из последнего уравнения СЛАУ (14) имеем
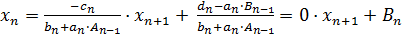 , так как
, так как 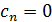 , при i=n;
, при i=n;
т.е. 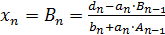 .
.
Дата добавления: 2016-03-04; просмотров: 3012;
