Этап прямого хода закончен.

Этап обратного хода:

Из последнего уравнения имеем .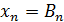

Далее обратный ход осуществляется в соответствии с формулой (15):

,

,

………

,

.

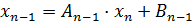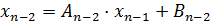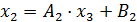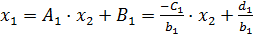Этап обратного хода завершен.

Получено решение СЛАУ (14) методом скалярной прогонки.

Число операций в методе скалярной перегонки равно при n=20 равно 8n+1=161 операций

Число операций в методе Гауса равно .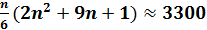

По экономичности методов вывод ясен!

Сравнение прямых и итерационных численных методов

Решения СЛАУ

Использование прямых и итерационных численных методов регешения СЛАУ зависит от величины порядка СЛАУ. Теоретические и экспериментальные исследования показали:

1. При порядке СЛАУ меньше 100 по точности решения выше и время решения меньше у прямых методов решения СЛАУ по сравнению с итерационными методами решения СЛАУ.

2. При порядке СЛАУ 100 и больше точность решения СЛАУ итерационными методами сравнивается с точностью решения прямыми методами, а время решения итерационными методами меньше, чем прямыми методами.

Это объясняется двумя причинами:

а) при больших порядках СЛАУ существенно увеличивается ошибка округления в прямых методах,

б) итерационные методы менее чувствительны к ошибкам округления, так как в этих методах ошибка решения оценивается априори и является управляемой. Таким образом, при n 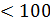нужно применять прямые методы решения СЛАУ, а при n 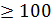нужно применять итерационные методы решения СЛАУ. Однако, сравнивая прямые и итерациорнные методы надо иметь ввиду, что область применения прямых методов больше, чем область применения итерационных методов. Это объясняется тем, что область применения прямых методов определяется только условиями теоремы Кронекера-Капелли, а область применения итерационных методов определяется и условиями теоремы Кронекера-Капелли, и дополнительно условиями сходимости итерационного процесса к точному решению СЛАУ.