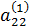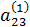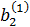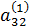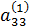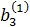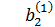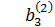Метод исключения Гаусса.
Система линейных алгебраических уравнений (СЛАУ)общего вида в векторно-матричной форме записывается следующим образом
А  Х = В, (*)
Х = В, (*)
где А – квадратная матрица размером 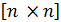 ;
;
Х = 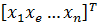 - вектор искомых параметров размером
- вектор искомых параметров размером 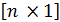 ;
;
В = 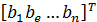 - вектор правых частей размером
- вектор правых частей размером 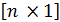 .
.
Существование решения любой СЛАУ определяется условиями теоремы Кронекера-Капелли:
1). Для того чтобы СЛАУ (*) имела решение, необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы.
2). Если ранг основной и расширенной матриц совпадают с числом неизвестных, то СЛАУ (*) имеет единственное решение.
3). Если ранг r основной и расширенной матриц меньше числа неизвестных (r 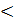 n), то СЛАУ (*) имеет более одного решения. В этом случае число «свободных» неизвестных, через которые выражаются остальные неизвестные, равно n-r.
n), то СЛАУ (*) имеет более одного решения. В этом случае число «свободных» неизвестных, через которые выражаются остальные неизвестные, равно n-r.
Существуют различные модификации метода Гаусса – метод исключения, метод последовательной подставки и др. Наибольшее распространение получил метод исключения. Этот метод и будем изучать.
Принцип метода исключения Гаусса включает прямой ход, где основная квадратная матрица заданного уравнения преобразуется с помощью эквивалентных действий в верхнюю или нижнюю треугольные матрицы, и обратный ход, где определяются значения искомых переменных. Рассмотрим решение СЛАУ методом исключения Гаусса на примере.
Дана СЛАУ:
a11·x1 + a12·x2 + a13·x3 = b1,
a21·x1 + a22·x2 + a23·x3 = b2,
a31·x1 + a32·x2 + a33·x3 = b3.
Прямой ход:
Составит расширенную матрицу:
| Первый шаг
-a21/ a11; -a31/ a11
a11≠ 0!
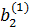 =b2+b1·(-a21/ a11) =b2+b1·(-a21/ a11)
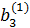 =b3+b1·(-a31/ a11) =b3+b1·(-a31/ a11)
|
матрица системы А
| Второй шаг
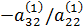
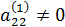
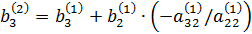
|
| Прямой ход закончен Получили СЛАУ с треугольной матрицей |
Обратный ход:
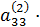 x3=
x3= 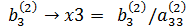 ;
;
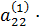 x2+
x2+ 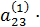 x3=
x3= 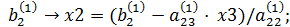
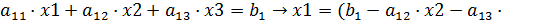
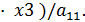
Обратный ход закончен!
Заданная СЛАУ решена методом исключения Гаусса.
Замечание 1. Если все элементы какой либо строки матрицы системы А в результате преобразования стали равными нулю, а правая часть b не равна нулю, то СЛАУ несовместна, поскольку не выполняются условия теоремы Кронеккера-Капели.
Замечание 2. Если элементы какой-либо строки матрицы системы А и правая часть (b) стали равными нулю, то СЛАУ совместна, но имеет бесконечное множество решений, которые получаются по методу Гаусса для СЛАУ порядка r, где r– ранг матрицы исходной СЛАУ.
Дата добавления: 2016-03-04; просмотров: 774;