Метод простой итерации

Дана система линейных уравнений

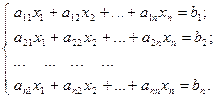
Предположим, что диагональные элементы а_ii, i = 1- n не равны 0. В любом случае строки и столбцы можно поменять местами так, чтобы диагональные элементы не были равны 0. Разделим каждую строку на ее диагональный элемент: первую строку на 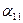, вторую строку на 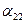и т.д. Получим следующую систему

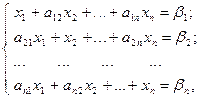
где ; .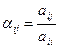

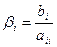В матричном виде эту систему можно записать

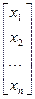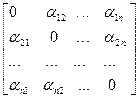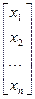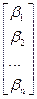+ х = или .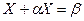

Отсюда 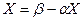. (1)

Выполненная выше операция называется приведением системы линейных уравнений к виду, удобному для итераций.

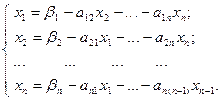
Зададим произвольное начальное значение всех неизвестных корней системы 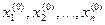(в матричном виде Х = Х⁽⁰⁾)и подставим это значение в правую часть системы уравнений (1).

Вычислим ,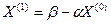

где Х⁽⁰⁾ – начальное (исходное) приближение к корням системы уравнений,

Х⁽¹⁾ - первое приближение к корням системы уравнений.

Затем процесс повторим, подставив найденные на первой итерации значения Х=Х⁽¹⁾ в правую часть системы уравнений и вычислим вторые приближения корней

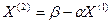. И так далее.

Итерационный процесс повторяем до тех пор, пока на какой-нибудь к-й итерации не выполнится условие

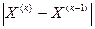<ε,

где ε – заданная точность определения корней системы.

Поскольку в вектор Х входит n неизвестных, то условие окончания итерационного процесса, должно быть выполнено для всех n корней.

Пример: дана система линейных уравнений

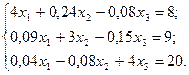
Приведем систему уравнений к виду, удобному для итерации

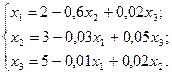
Зададим начальные приближения к корням равными нулю 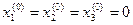и точность расчета ε = 0,001.

Начнем итерационный процесс вычисления корней.

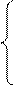1 итерация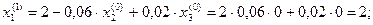

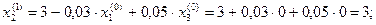
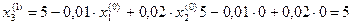
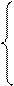2 итерация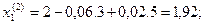

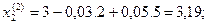
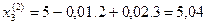
и т.д. до выполнения условий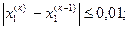

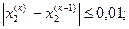
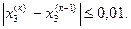
Вычисления сведем в таблицу

№ итерации (к)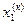
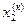
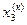
	1,92	3,19	5,04
	1,9094	3,1944	5,0446
	1,9092	3,1949	5,0448

Примечание: число цифр после запятой в вычисляемых приближениях к корням надо брать на один порядок больше чем в заданной точности ε.