И методах их решения
 Для примера приведем нелинейные уравнения балансов мощностей в узлах электрической сети, составленных по методу узловых напряжений (без вывода).
Для примера приведем нелинейные уравнения балансов мощностей в узлах электрической сети, составленных по методу узловых напряжений (без вывода).
Ргiи Qгi - активная и реактивная мощности, генерируемые в i-м узле;
Рнi и Qнi - активная и реактивная мощности нагрузки в i-м узле;
Руi и Qуi - активные и реактивные потоки мощности из узла j к узлу j.
Уравнения балансов активных и реактивных мощностей в узле i
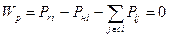 ; ;
|
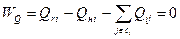 , ,
|
где 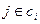 означает, что узел j‚ принадлежит множеству всех узлов, которые связаны с узлом i.
означает, что узел j‚ принадлежит множеству всех узлов, которые связаны с узлом i.
Формулы для потоков активной и реактивной мощностей от узла к узлу j следующие:
Применяются две системы координат, в которых могут проводиться расчеты:
1) прямоугольная система координат (в комплексном виде);
2) полярная система координат (через тригонометрические функции).
В полярной системе координат выражения для потоков мощности имеют следующий вид:
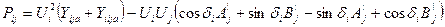
|
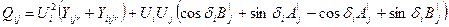
|
где 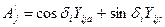 ;
;
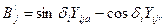 ;
;
Y – заданные проходимости схемы замещения системы;
P, Q, U, 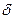 - параметры режима, часть из них известна (обычно это мощности нагрузок в узлах, напряжение и угол в базисном узле), остальные являются искомыми переменными, которые следует определить в результате расчета.
- параметры режима, часть из них известна (обычно это мощности нагрузок в узлах, напряжение и угол в базисном узле), остальные являются искомыми переменными, которые следует определить в результате расчета.
Подчеркнем, что нелинейность в уравнениях выражается как наличием в них степеней второго порядка, так и наличием тригонометрических функций.
Для решения систем нелинейных уравнений используются только итерационные методы. В том числе для решения систем нелинейных уравнений могут использоваться методы простой итерации и Зейделя при условии их сходимости.
Пример: дана система нелинейных уравнений

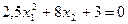 ;
;
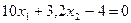 .
.
Приведем к виду удобному для итерации

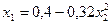 ;
;
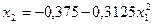 .
.
Результаты расчетов обоими методами сведем в таблицу (ε=0,001)
| Метод простой итерации | Метод Зейделя | |||||
| № итерации | х1 | х2 | № итерации | х1 | х2 | |
| 0,4 | -0,375 | 0,4 | -0,425 | |||
| 0,355 | -0,425 | 0,3422 | -0,412 | |||
| 0,3422 | -0,415 | 0,3457 | -0,41235 | |||
| 0,345 | -0,412 | 0,3456 | ||||
| 0,3457 | -0,4122 |
Нелинейные уравнения, составленные для расчетов режимов, обычно сложнее чем в приведенном примере и их не всегда можно решить этими методами. Гораздо лучшую сходимость для решения нелинейных уравнений и вследствие этого большее применение имеет метод Ньютона. Но этот метод имеет более сложную вычислительную процедуру.
Метод Ньютона /2/ (называемый также методом линеаризации или методом касательных) применяется для решения системы нелинейных уравнений. Он эффективен, если известно достаточно хорошее приближение к корням системы нелинейных уравнений.
Дата добавления: 2016-02-16; просмотров: 1076;
