Метод простой итерации (метод последовательных повторений)

Для применения метода простой итерации следует исходное уравнение f(x) = 0 преобразовать к виду, удобному для итерации x = j(x). Это преобразование можно выполнить различными способами. Функция j(x) называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:

x⁽ⁿ⁺¹⁾ = j(x⁽ⁿ⁾).

Теорема о сходимости метода простой итерации. Пусть в некоторой s - окрестности корня x* функция j(x) дифференцируема и удовлетворяет неравенству |j’(x)|£ q, где 0£ q< 1 — постоянная. Тогда независимо от выбора начального приближения из указанной s - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической последовательности и справедлива оценка погрешности:

, .

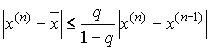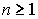Критерий окончания итерационного процесса. При заданной точности ε >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство

.

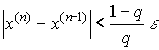Если величина 0 < q £ 0,5, то можно использовать более простой критерий окончания итераций:

.

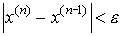Внимание. Ключевым моментом в применении метода простой итерации является эквивалентное преобразование уравнения к новой форме.

Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду x = x - a f(x). Предположим также, что производная f’ непрерывна и положительна на заданном отрезке, т.е. справедливо выполнение неравенства m£ f’(x)£ M на отрезке [a,b]. Тогда при выборе итерационного параметра a = 2/(m+M) метод сходится и значение

е .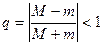

Если же известна для производной только оценка сверху, то положим a = 1/ M и q = 1 – m/M – тоже менее единицы.

Примечание. Для практического знакомства с технологий численного решения нелинейного уравнения методом простой итерации выполните лаб. работу № 5.