Метод Ньютона (метод касательных)

Расчетная формула метода Ньютона имеет вид:

.

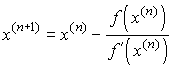Геометрически метод Ньютона означает, что следующее приближение к корню x⁽ⁿ⁺¹⁾ есть точка пересечения с осью ОХ касательной, проведенной к графику функции y = f(x) в точке (x⁽ⁿ⁾, f(x⁽ⁿ⁾)).

4.3.1.Теорема о сходимости метода Ньютона

Пусть x* - простой корень уравнения f(x) = 0, в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая σ - окрестность корня x*, что при произвольном выборе начального приближения x⁽⁰⁾ из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка

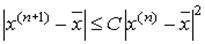, где , .

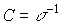Критерий окончания итерационного процесса: при заданной точности e > 0 вычисления следует вести до тех пор пока не окажется выполненным неравенство

.

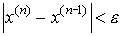Примечание. Для практического знакомства с технологий численного решения нелинейного уравнения методом Ньютона выполните лаб. работу № 5.

Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня x*. Неудачный выбор может дать расходящуюся итерационную последовательность.