Метод дихотомии (деления отрезка пополам)

Лекция 4

Численные методы решения нелинейных уравнений

Содержание

· Определение простого и кратного корней.

· Постановка задачи приближенного решения нелинейного уравнения.

· Алгоритм метода дихотомии (деления отрезка пополам)

· Теорема о сходимости метода хорд.

· Алгоритм метода Ньютона.

· Теорема о сходимости метода Ньютона

· Алгоритм метода простой итерации

· Теорема о сходимости метода простой итерации

· Приведение уравнения к виду, удобному для итераций.

Введение

Пусть рассматривается уравнение

f(x) = 0.

Корнем уравнения называется значение x*, при котором f(x*) = 0.

Корень x* называется простым, если f’(x*) ¹ 0, в противном случае корень называется кратным. Целое число m называется кратностью корня x*, если f^(k)(x*) = 0 для k=1,2,3,…,m-1 и f^(m)(x*) ¹ 0.

Постановка задачи. Вычисление приближенного значения корня с точностью e предполагает поиск такого значения x, что

ôx – x^*ô< e.

Решение задачи разбивается на два этапа:

· на первом этапе осуществляют локализацию корней,

· на втором этапе производят итерационное уточнение корней.

На этапе локализации корней находят достаточно узкие отрезки (или отрезок, если корень единственный), которые содержат один и только один корень уравнения f(x)=0. На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.

Примечание. Для практического знакомства с процедурами локализации корней выполните лаб. работу № 4.

Метод дихотомии (деления отрезка пополам)

Пусть[a,b] – отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков, т.е. f(a)_* f(b)< 0.

Алгоритм метода дихотомии состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Опишем один шаг итераций метода.

Пусть на k-ом шаге найден отрезок [a^(k), b^(k)] такой, что f(a^(k))·f(b^(k)) < 0. Найдем середину отрезка

.

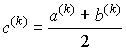Если f(c^(k)) = 0, то c^(k) - корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:

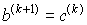, , если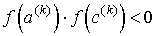

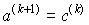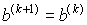, , если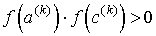

Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2ε, то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.