Жидкость на жидкости
Некоторые жидкости, например, масло, вода, ртуть, не смешиваются между собой. Если налить такие жидкости в один сосуд, то они будут располагаться слоями одна над другой. При этом внизу будет находиться жидкость, имеющая наибольшую плотность. Так, если налить в один сосуд воду и ртуть, то слой ртути будет снизу, а слой воды – сверху. Если же налить в один сосуд воду и подсолнечное масло, то снизу будет вода, а сверху масло.
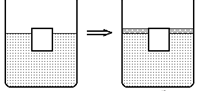
Автор:На поверхности воды в сосуде плавает деревянный кубик (рис. 29.6,а). Изменится ли глубина погружения кубика в воду, если сверху налить слой подсолнечного масла (рис. 29.6,б)?
 а) б)
а) б)
|  в)
в)
|
Рис. 29.6
Читатель: Я думаю, глубина погружения кубика в воду не изменится, ведь налитое масло будет давить на кубик только с боков, а сверху и снизу никаких новых сил не появится.
Автор: Не совсем так. Слой масла окажет давление на поверхность воды, и это давление по закону Паскаля передастся во все точки под водой без изменения. А значит, это дополнительное давление передастся и нижнему основанию кубика (рис. 29.6,в). Следовательно, появится дополнительная сила, действующая снизу вверх на нижнее основание кубика. Ясно, что под действием этой силы он немного поднимется вверх, и глубина его погружении в воду уменьшится.
Пусть теперь деревянный кубик плавает на границе раздела между слоями воды и масла, как показано на рис. 29.6,б. Изменится ли глубина погружения кубика в воду, если сверху еще долить масла?
Читатель: Я думаю, да. Кубик будет подниматься над поверхностью воды, ведь чем больше толщина слоя масла, тем большее давление масло будет оказывать на поверхность воды, а значит, тем больше будет сила давления на нижнюю грань кубика.
Автор: А вот и нет! Действительно, на нижнюю грань кубика давление возрастет, но ведь на столько же возрастет давление и на верхнюю грань кубика. Поэтому результирующая добавка будет равна нулю.
Задача 29.4.Поверх ртути в сосуде налита вода. Кусок гранита объёмом V = 120 см3 плавает у границы раздела этих жидкостей, при этом гранит полностью накрыт водой (рис. 29.7). Какой объём гранита V1 погружен в воду?
| V = 120 см3 | Решение. Плотности: гранита rт = 2,7 г/см3, воды r1 = 1,000 г/см3, ртути r2 = 13,6 г/см3.
Запишем условие плавания гранита: FA = Fт. Сила Архимеда в этом случае состоит из двух сил: силы Архимеда 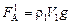 , действующей на гранит со стороны воды, и силы Архимеда , действующей на гранит со стороны воды, и силы Архимеда 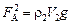 , действующей на гранит со стороны ртути. Общая сила Архимеда составит:
FА = , действующей на гранит со стороны ртути. Общая сила Архимеда составит:
FА = 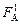 + + 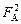 = = 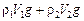 . .
|
| V1 = ? | |
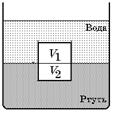 Рис. 29.7 Рис. 29.7
|
Сила тяжести, действующая на гранит, Fт = ттg = rтVg.
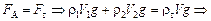
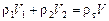 . (1)
. (1)
Учтём, что V = V1 + V2 Þ V2 = V – V1. Подставим в формулу (1) значение V2 = V – V1 и решим полученное уравнение относительно V1:

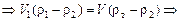
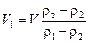 . (2)
. (2)
Подставим численные значения:
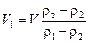 =
=  =
=
= 103,8 см3 » 1,0×102 см3.
Ответ: 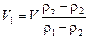 » 1,0×102 см3.
» 1,0×102 см3.
СТОП! Решите самостоятельно: А3, В19, С15.
Дата добавления: 2016-04-11; просмотров: 3244;
