Проблема подводной лодки
Автор: Как Вы считаете, может ли подводная лодка, находящаяся на небольшой глубине, безопасно для себя ложиться на дно?
Читатель: Честно говоря, у меня тут есть сомнение: а будет ли действовать на подводную лодку сила давления воды снизу, если дно лодки вплотную прилегает к грунту? Ведь если этой силы снизу не будет, то лодка не сможет всплыть на поверхность, потому что сверху на неё действует сила давления воды, которая прижимает её ко дну, кроме того, её прижимает ко дну сила тяжести.
Автор: Ваши опасения вполне обоснованы, тем более, что ко дну ее прижимает еще и сила атмосферного давления. Тут все дело в том, какой грунт. Если песчаный, то вода будет просачиваться между песчинками, и под дном подводной лодки будет тонкая прослойка воды, которая и обеспечит давление воды снизу. А вот если грунт глинистый, то лодка может увязнуть в этой глине, так как вода действительно не будет поступать под днище лодки, а значит, на лодку не будет действовать выталкивающая сила Архимеда. Такая ситуация для подводной лодки даже на небольшой глубине означает неминуемую гибель.
СТОП! Решите самостоятельно: В1, В3, В4, С1–С3.
Плавание тел
Задача 29.1.Плоская льдина толщиной h = 1,0 м плавает в воде. Определите толщину подводной части льдины (рис. 29.3).
| h = 1,0 м | 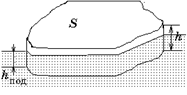 Рис. 29.3 Рис. 29.3
|
| hпод = ? | |
Решение. Как известно, плотность воды rж = 1,00 г/см3, плотность льда rт = 0,90 г/см3. Пусть площадь льдины равна S. Поскольку льдина находится на плаву, то
Fт = FА Þ ρтVg = ρжVвытg Þ
rтV = rжVвыт, (1)
где rт – плотность тела (льда); V – объём льдины; rж – плотность жидкости (воды); Vвыт – объём вытесненной воды.
Как видно из рис. 29.3, V = Sh, Vвыт = Shпод. Тогда из формулы (1) получим:
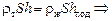
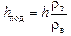 .
.
Подставим численные значения:
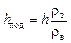 = 1,0 м
= 1,0 м 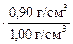 = 0,90 м » 90 см.
= 0,90 м » 90 см.
Ответ: 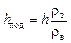 » 90 см.
» 90 см.
СТОП! Решите самостоятельно: А1, В5, В7, С6.
Взвешивание в воде
Задача 29.2. Золотая ли корона? По легенде царь города Сиракузы поручил Архимеду проверить, из чистого ли золота сделана ювелиром царская корона. Архимед знал, чему равна плотность золота и плотность воды. Знал он также открытый им закон. Взвесив корону один раз в воде, а другой раз в воздухе, он по результатам этих двух взвешиваний сумел определить плотность короны.
Пусть в воздухе корона весила Р1 = 20,0 Н, а в воде Р2 = 18,0 Н. Определите по этим данным плотность короны.
| Р1 = 20,0 Н Р2 = 18,0 Н | Решение. Введем следующие обозначения: rк – искомая плотность короны; rв = 1,00 г/см3 – плотность воды; V – объём короны; тк – масса короны. Тогда тк = rкV, вес короны в воздухе |
| rк = ? | |
Р1 = ткg = rкVg.
Плотностью воздуха мы здесь пренебрегаем, так как она значительно меньше плотности воды. Вес короны в воде
Р2 = ткg – FА= rкVg – rжVg = Vg(rк – rж).
Итак, мы получили два уравнения:
Р2 = 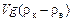 , (1)
, (1)
Р1 = rкVg. (2)
Разделим первое уравнение на второе:
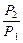 =
=  =
= 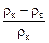 .
.
Итак: 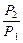 =
= 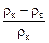 . Из этого уравнения найдем rк:
. Из этого уравнения найдем rк:
 =
=  » 10 г/см3.
» 10 г/см3.
Ответ:  » 10 г/см3.
» 10 г/см3.
СТОП! Решите самостоятельно: В10, В11, В13.
Дата добавления: 2016-04-11; просмотров: 1584;
