Почему возникает сила Архимеда?

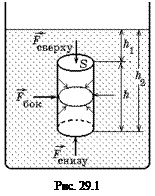Рассмотрим цилиндр высотой h, целиком погружённый в жид­кость (или газ) плотностью r_ж. Пусть площадь основания цилин­дра равна S (рис. 30.1). Попробуем вычислить значение силы Архимеда.

Пусть верхнее основание цилиндра на­ходится на глубине h₁, а нижнее — на глубине h₂ = h₁ + h. На глубине h₁ гидростатическое дав­ление равно р₁ = rgh₁, а на глубине h₂ р₂ = rgh₂.

Сразу заметим, что силы, дей­ствующие на боковую поверхность ци­линдра, 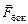будут только сжимать наш цилиндр. Поскольку они направлены горизонтально, сдвинуть его вверх или вниз эти силы не могут.

На верхнее основание цилиндра действует сила:

,

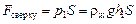а на нижнее основание — сила:

.

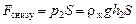Эти силы направлены в противоположные стороны, причем поскольку h₂ > h₁, то F_снизу > F_сверху. Равнодействующая этих сил как раз и является силой Архимеда F_А, которая стремится вытолкнуть тело на поверхность жидкости:

F_A = F_снизу – F_сверху = r_жgh₂S – r_жgh₁S =

= r_жgS(h₂–h₁) = r_жgSh.

Поскольку Sh = V – объём нашего цилиндра, который равен объёму вытесненной им жидкости, то, вводя обозначение V_выт = Sh, получим уже известную нам формулу (29.1) для вычисления силы Архимеда:

F_A = r_ж gV_выт .

Поскольку r_жV_выт = т_ж – масса вытесненной цилиндром жид­кости, то F_А = т_жg, а эта величина, как мы знаем, равна весу вытесненной жидкости при условии, что жидкость по­коится.

Таким образом, мы доказали, что сила Архимеда F_А действи­тельно равна весу вытесненной жидкости или газа, и получили формулу (29.1), позволяющую рассчитывать силу Архимеда.

Читатель: Вы рассмотрели случай, когда тело целиком находится в жидкости. А как найти силу Архимеда, если часть тела находится над поверхностью жидкости, например, как на рис. 29.2?

Рис. 29.2

Автор: Давайте рассмотрим и такую си­туацию. Пусть h – высота подвод­ной части нашего цилиндра, тогда на нижнее основание действует со стороны жидкости сила: Fснизу = рS = rжghS = rжgVвыт, где Vвыт – объём подводной части цилиндра, равный объёму вытесненной цилиндром жидкости. А сверху на цилиндр со стороны жидкости никаких сил не действует. Поэтому в

данном случае F_cнизу – это и есть сила Архимеда:

F_A = F_снизу =r_жgV_выт.

Как видите, получилось то же значение, что и в формуле (29.1).

Читатель: А почему мы не учли силу атмосферного давления?

Автор: Давайте разберёмся. Сначала рассмотрим случай, когда наш цилиндр целиком погружён в жидкость (см. рис. 29.1).

В этом случае атмосферное давление является внешним для жидкости и по закону Паскаля передается во все точки жидкости без изменений. Поэтому атмосферное давление даст дополнительное одинаковое по величине давление на верхнее и нижнее основания. Силы, обусловленные этим давлением, будут равны по величине и противоположны по направлению и поэтому компенсируют друг друга. Следовательно, учет атмосфер­ного давления никак не повлияет на величину выталкивающей силы.

Если же тело выступает над поверхностью жидкости (см. рис. 29.2), то, строго говоря, атмосферное давление на верхнее основание цилиндра будет чуть меньше, чем атмосферное давление на поверхность жид­кости, которое по закону Паскаля передается нижнему основанию. Разница между этими давлениями

,

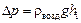где r_возд – плотность воздуха. Но поскольку плотность воздуха значительно меньше плотности жидкости, этой разницей можно пренебречь и счи­тать атмосферное давление на верхнее и нижнее основания цилиндра одинаковым.

Другое дело, если речь идет о воздушном шаре. Там именно раз­ность сил атмосферного давления сверху и снизу как раз и является силой Архимеда.

Автор: Как Вы считаете, справедлива ли формула (29.1) для шарика, плавающего в стакане с водой в ускоряющемся лифте?

Читатель: Я думаю, что нет, так как при движении лифта, например, с ускорением а, направленным вверх, вес вытесненной жидкости возрастет и станет Р_ж = т_ж(g + а), а значит, возрастет и сила Архимеда.

Автор: Совершенно верно. Но это не единственный случай, когда формула (29.1) «в чистом виде» неверна.