Как и почему появился язык математической логики.
Приведем описание поля деятельности современной математики: «Математика изучает объекты, свойства которых точно сформулированы». Хотя само описание говорит о точных формулировках, в нем требуют уточнения, прежде всего, слова «точно сформулированы», затем «объекты» и «свойства».
Итак, какие же формулировки можно считать точными? Например, предложение «Он встретил её на поляне с цветами» имеет три различных истолкования.
Пытаясь застраховаться от такой неоднозначности, математики с самого начала стремились формулировать теоремы и доказательства на как можно более четком, хотя и бедном, диалекте естественного языка. Словарный запас этого диалекта постоянно расширяется, но основные формы предложений, связки, союзы остаются практически теми же, что были выработаны еще в античные времена. Долгое время считалось, что математический диалект состоит из строго сформулированных предложений. Но уже в средние века развитие алгебры привело к тому, что формулировки теорем часто становились всё длиннее и неудобнее. Соответственно, доказательства становились труднее.
Выход был найден, когда заметили, что часть математического языка может быть заменена несколькими условными знаками. Например, предложение «Квадрат первого, сложенный с квадратом второго и удвоенным произведением первого на второе, равен квадрату суммы первого со вторым» записывается кратко х2+2ху+у2=(х+у)2. Это стало первым этапом уточнения математического языка: был создан символизм арифметических выражений, их равенств и неравенств. Однако более сложные математические утверждения все еще записывались на обычном языке с включениями формул.
Язык[1] математической логики[2], ставший символическим языком современной математики, возник в тот момент, когда неудобство математического языка для нужд математики было окончательно осознано. Новый символизм, также как и символизм алгебраических выражений, прояснил механическую природу многих преобразований и позволил дать простые алгоритмы их осуществления. Вместе с тем появилась возможность строго ответить на вопрос: «Что есть точно сформулированное высказывание?» Это высказывание, которое может быть однозначно переведено на символический язык математики.
К чему привело появление языка математической логики. Прежде всего, это привело к появлению алгебры логики[3]. Частным случаем алгебры логики является Булева алгебра[4]. В алгебре Буля область определения функции и область значений переменных ограничиваются 0 и 1. То есть любая переменная, и любая функция в булевой алгебре могут принимать только 2 значения: 0 или 1, что трактуется как «ложь» или «истина», соответственно.
Как мы знаем из истории становления и развития информатики, появлению компьютеров способствовало развитие математики (в области создания счетных машин) и физики (в области применения электромагнетизма). Алгебра Буля наилучшим образом объединила физику и математику. С одной стороны, 0 и 1 представляют алфавит двоичной системы счисления, с помощью которой можно выразить любое число и даже слово. А с другой стороны, те же 0 и 1 обозначают отсутствие или наличие тока в сети, направление магнитного поля в магнетиках, используемых в качестве материала, из которых изготавливают запоминающие устройства компьютеров и так далее.
В итоге язык математической логики определил направление развития информатики в области создания ЭВМ, а развитие физики и электротехники способствовало появлению современных компьютеров.
Так, например, американский логик Чарльз Сандерс Пирс первым осознал, что бинарная логика имеет сходство с работой электрических переключательных[5] (контактных) схем.
Появление вакуумных и полупроводниковых электронных приборов создало возможность построения логических элементов с быстродействием от 1 миллиона переключений в секунду и выше. В электронных схемах логические элементы характеризуются не состоянием контактов, а наличием сигналов на входе и выходе элемента.
Таким образом, изучение алгебры логики и различных систем счисления является основой изучения науки информатики.
Система счисления
1.1 Классификация систем счисления
Система счисления– это способ представления чисел и совокупность приемов и привил, по которым числа записываются и читаются.
Существуют непозиционные и позиционные системы счисления.
В непозиционных системах счислениязначение цифры не зависит от её позиции в записи числа.
Примером может служить римская система: В числе X X X (тридцать) вес цифры X в любой позиции просто равен десяти.
В позиционных системах счислениявес каждой цифры изменяется в зависимости от её положения (позиции) в последовательности цифр в числе.
Например, в числе 333 (триста тридцать три) вес цифры 3 изменяется от её позиции. Если смотреть слева на право, то первая 3 стоит в позиции сотен и означает триста, вторая 3 – в позиции десятков и означает тридцать, а третья 3 находится в позиции единиц и означает просто три. Так 333 можно представить выражением:
300+30+3=3ž102+3ž101+3ž100
В дальнейшем мы будем работать с позиционными системами счисления.
Любая позиционная система счисления характеризуется своим основанием, т.е. количеством различных цифр, используемых для изображения чисел в данной системе счисления.
Возможно бесчисленное множество позиционных систем, т.к. за основание системы можно принять любое натуральное число - два, три, четыре, десять, шестнадцать, тридцать два, сорок и т.д. Название системы будет зависеть от основания.
Например, десятичная система счисления имеет основание десять (q=10) и для записи чисел используются десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Основание два (q=2) – система двоичная (0, 1), основание восемь (q=8) – система восьмеричная (0, 1, 2, 3, 4, 5, 6, 7) и т.д.
Однако, начиная с одинадцатиричной системы, где q=11 число 10 (где 1 относится уже к первому разряду, а 0 к нулевому) и цифра 10 изображаются одинаково, а имеют разный вес в системе. Для того чтобы не было путаницы, такие цифры заменяют буквами латинского алфавита по возрастанию.
Например:
а) Двенадцатеричная система – q=12
Используются цифры – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 следовательно две последние цифры заменяем буквами, т.е. будем иметь ряд цифр и букв:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
Число в двенадцатеричной системе будет записываться следующим образом, например, 1A23, B12
б) Шестнадцатеричная система – q=16
Используются цифры – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 после замены буквами будем иметь ряд цифр и букв:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Представление числа в шестнадцатеричной системе – FFA12, 1DB8
Множество всех символов (цифр и букв), используемых для записи чисел в данной системе счисления – называется алфавитом системы счисления.
Таблица 1.1
Алфавиты систем счисления
| Система счисления | Основание | Алфавит |
| Десятичная | ||
| Двоичная | ||
| Троичная | ||
| Восьмеричная | ||
| Шестнадцатеричная | 0123456789АВСDЕF |
1.2 Понятие базиса системы счисления
Разряды числа указывают на позицию цифр в этом числе. Старшинство разрядов считается справа налево.
 | |||
 |
3 3 3
 |  |
Рис. 1.1 Представление разрядов в позиции цифр числа
Значение числа складывается как сумма цифр, составляющих число, умноженное на основание q системы в степени, обозначающей номер позиции этой цифры в числе.
Запись чисел в любой из систем счисления с основанием q можно представить в следующем виде:
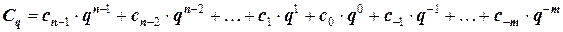 , (1)
, (1)
где 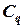 - число в q-ичной системе счисления;
- число в q-ичной системе счисления; 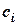 - цифры системы счисления;
- цифры системы счисления; 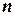 и
и 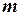 - число целых и дробных разрядов, соответственно.
- число целых и дробных разрядов, соответственно.
Например:
Число в двоичной системе счисления 1101,11; q=2.
| Разряды | 3 | 2 | 1 | 0 | -1 | -2 | |
| Число | 1, | = 1*23 + 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 |
Число в восьмеричной системе счисления 672,721; q=8.
| Разряды | 2 | 1 | 0 | -1 | -2 | -3 | |
| Число | 2, | =6*82 +7*81 +2*80 + 7*8-1 + 2*8-2 +1*8-3 |
Последовательность степеней основания называютбазисом системы счисления.
«Разложить число по базису системы счисления» - т.е. представить число в развернутой форме.
Например:
101,012 = 1 • 22 + 0 • 21 +1 • 20 + 0 • 2¯1+ 1 • 2¯2;
673,28 = 6ž82 + 7ž81+3ž80 + 2ž8¯1;
15FС16 = 1ž163+5ž162+ Fž161 + Сž160=
= 1ž163+5ž162+15ž161+12ž160.
1.3 Перевод чисел из любой системы счисления
в десятичную систему
Представление чисел в развернутой форме одновременно является способом перевода чисел в десятичную систему из любой другой позиционной системы счисления. Достаточно подсчитать результат по правилам десятичной арифметики.
Например:
101,012=1ž22+0ž21+1ž20+0ž2¯1+1ž2¯2 =4 + 1 + 1/4= 5,2510
673,28=6ž82+7ž81+3ž80+2ž8¯1= 384+56+3+2ž1/8 =443,2510
15FС16= 1ž163 +5ž162 + 15ž161 + 12ž160 = 562810
Например: Найдем сумму чисел в десятичной системе счисления
1112 +1118 +11116.
1) 1112 = 1 • 22 +1 • 21 + 1 • 20 = 4 + 2 + 1 = 710;
2) 1118 = 1 • 82 +1 • 81 +1 • 80 = 64 + 8 +1 = 7310;
3) 11116 = 1ž162+1ž161 +1ž160 =256+16+1 = 27310.
В результате получим:
1112 +1118 +11116 = 7 + 73 + 273 = 35310.
1.4 Перевод десятичных целых чисел в другие системы счисления (метод поэтапного деления)
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо:
1. Разделить с остатком (“нацело”) число N на q.
Полученный остаток дает цифру, стоящую в нулевом разряде q-ичной записи числа N.
2. Полученное частное снова разделить на q и снова запомнить полученный остаток - это цифра первого разряда, и т.д.
3. Такое последовательное деление продолжается до тех пор, пока частное не станет меньше q.
4. Представлением числа N в новой системе счисления будет последовательность остатков деления, записанных в порядке, обратном порядку их получения. Если деление числа, осуществлять методом столбика, тогда цифрами искомого числа являются остатки от деления, выписанные слева направо начиная с последнего полученного остатка.
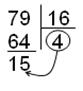
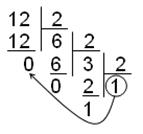 Например: 1210 ® ?2 1210 ® ?8 7910 ® ?16
Например: 1210 ® ?2 1210 ® ?8 7910 ® ?16
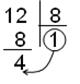
т.к. 15 – это F, то
1210 ® 11002 1210 ® 148 7910 ® 4F16
1.5 Алгоритм разложения числа по базису новой системы счисления (метод разностей)
Для быстрого перевода десятичного числа в двоичный код (битовый, байтовый формат) можно использовать метод разностей
Таблица 1.2
Соответствие степени и разряда
| Номера разрядов | |||||||||
| Десятичные числа | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Один байт |
1. Найти по таблице 1.2 степень новой системы, ближайшую по величине к исходному числу, но не больше исходного числа - это будет первый член суммы.
2. Найти разность между исходным числом и степенью.
3. Найти по таблице степень, ближайшую к разности, - это второй член суммы.
4. Найти разность между числом, из которого выделяли степень, и степенью.
5. Так поступать, пока разность не станет равной числу, входящему в алфавит искомой системы.
Например:
а) Переведем 4510 с помощью таблицы в двоичную систему.
1) Число 45 находится в интервале 64(26)>45>32(25), следовательно, первый член суммы будет 32 и максимальный номер разряда будет 5, а бит числа 1.
2) Найдем разность 45-32=13, а 16(24)>13>8(23), тогда при четвертом разряде бит числа будет равен 0, а при третьем – 1.
3) Теперь 45-32-8=5, где 8(23)>5>4(22), следовательно, при разряде 2 бит числа будет равен 1.
4) 45-32-8-4=1, тогда при разряде 0 бит числа будет 1.
| Номера разрядов | ||||||||
| Десятичное число | ||||||||
 45 45
| ||||||||
| биты числа |
Ответ: 4510 = 1011012
б)Перевести число 10110 в двоичную систему счисления.
10110 = 6410 + 3210 + 410+110 = 11001012
1.6 Связь между двоичной, восьмеричной и
шестнадцатеричной системами счисления
Дата добавления: 2016-04-11; просмотров: 788;
