Перевод чисел из шестнадцатеричной в восьмеричную систему
Для того чтобы перевести число из шестнадцатеричной в восьмеричную систему:
1. Необходимо это число представить в двоичной системе.
2. Затем разделить получившееся число в двоичной системе на триады и перевести его в восьмеричную систему.
Например:
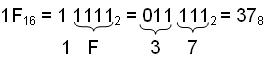
1.7 Алгоритм преобразования правильных дробей из любой системы счисления в десятичную систему
Перевод в десятичную систему числа С, как целого так и дробного, записанного в q-ичной системе счисления осуществляется с помощью разложения числа по базису по формуле 1 (см. разд. 1.2).
Однако для преобразования правильных дробейможно использовать следующий способ:
1. Цифру младшего разряда дроби 0,Аq разделить на основание q. К полученному частному прибавить цифру следующего (более старшего) разряда числа 0,Аq.
2. Полученную сумму вновь следует разделить на q и вновь прибавить цифру следующего разряда числа.
3. Так поступать, пока не прибавится цифра старшего разряда дроби.
4. Полученную сумму еще раз разделить на q и к результату приписать запятую и ноль целых.
Например:Переведем в десятичную систему счисления дроби:
| a). | 0,11012 | б). | 0,3568 |
| 1/2 + 0 = 0,5 | 6/8+5 = 5,75 | ||
| 0,5/2 + 1 = 1,25 | 5,75/8 + 3 = 3,71875 | ||
| 1,25/2 + 1 = 1,625 | 3,71875/8 = 0,46484375 | ||
| 1,625/2 = 0,8125 | |||
| Ответ:0,11012 = 0,812510 | Ответ: 0,3568 = 0,4648437510 | ||
1.8 Алгоритм преобразования правильных десятичных дробей в любою другую систему счисления
1. Умножить данное число на новое основание р.
2. Целая часть полученного произведения является цифрой старшего разряда искомой дроби.
3. Дробная часть полученного произведения вновь умножается на р и целая часть результата считается следующей цифрой искомой дроби.
4. Операции продолжать до тех пор, пока дробная часть не окажется равной нулю либо не будет достигнута требуемая точность.
5. Предельная абсолютная погрешность перевода числа D равняется q-(k+1)/2, где k- количество знаков после запятой.
Например:Переведем десятичную дробь 0,375 в двоичную, троичную и шестнадцатеричную систему счисления. Перевод выполнить с точностью до третьего знака.
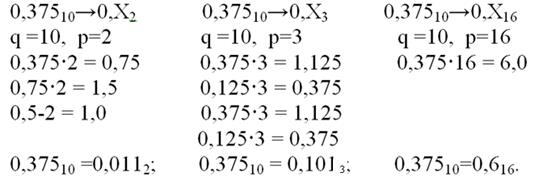
Например:Переведём число 0,3610 в двоичную, восьмеричную и шестнадцатеричную системы:
Для записи удобно использовать такую форму:
Перевод в Перевод в Перевод в
двоичную с/сч. восьмеричную с/сч. шестнадцатеричную
 0, 0,
| x36 | 
| 0, | x 36 | 
| 0, | x 36 |
| x72 | x 88 | x 76 | |||||
| x44 | x 04 | x 16 | |||||
| x88 | x 32 | x 56 | |||||
| x76 | x 46 | x 96 | |||||
| x52 | x 68 | x 36 | |||||
Ответ:
0,3610 = 0,0101112 с предельной абсолютной погрешностью (2-7)/2=2-8
0,3610 = 0,2702358 с предельной абсолютной погрешностью
(8-7)/2=2-22
0,3610 = 0,5C28F516 с предельной абсолютной погрешностью
(16-7)/2=2-29
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной части по правилам, указанным выше.
1.9 Продвижение цифр в позиционных системах счисления
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
В основе любой позиционной системы счисления лежат одинаковые принципы построения и перехода от младшего к более старшему разряду.
Рассмотрим продвижение цифры в позиционной системе счисления.
Продвижением цифры называют замену её следующей по величине (путём прибавления единицы).
В десятичной системе счисления продвижение цифр выглядит следующим образом:
| 0+1 | 1+1 | 2+1 | 3+1 | 4+1 | 5+1 | 6+1 | 7+1 | 8+1 |
Продвижение старшей цифры означает замену её на 0 и переход на следующий разряд.
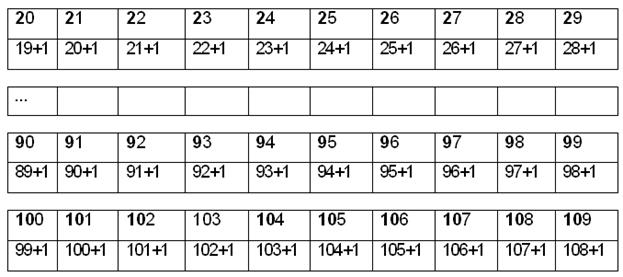
Продолжим продвижение цифр в знакомой нам десятичной системе счисления:
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 9+1 | 10+1 | 11+1 | 12+1 | 13+1 | 14+1 | 15+1 | 16+1 | 17+1 | 18+1 |
Снова дошли до цифры 9, поэтому происходит переход на более высший разряд, но в позиции 1-го разряда уже имеется цифра 1, поэтому происходит и продвижение цифры 1 первого разряда, т.е. 1+1=2 (два десятка). Так продвигаем цифры, пока в первом разряде не появится старшая цифра в системе счисления (в нашем примере это 9) теперь переход осуществляется на следующий разряд.
Рассмотрим теперь продвижение цифр в троичной системе счисления, т.е. q=3 (используются цифры 0, 1, 2) и старшая цифра 2.
| 0+1 | 1+1 | |
| 2+1 | 10+1 | 11+1 |
| 12+1 | 20+1 | 21+1 |
| 22+1 | 100+1 | 101+1 |
| 102+1 | 110+1 | 111+1 |
| и т.д. |
В жизни мы пользуемся десятичной системой счисления, вероятно, потому, что с древних времён считали по пальцам, а пальцев, как известно, десять на руках и ногах. Хотя в Китае долгое время пользовались пятеричной системой счисления.
Компьютеры используют двоичную систему потому, что для её реализации используются технические устройства с двумя устойчивыми состояниями (нет тока - 0; есть ток – 1 или не намагничен – 0; намагничен – 1 и т.п.). Так же применение двоичной системы счисления позволяет использовать аппарат булевой алгебры (см. раздел 2) для выполнения логических преобразований информации. Двоичная арифметика намного проще десятичной, но недостатком её является быстрый рост числа разрядов, необходимых для записи чисел.
Например: Продвинем цифры в двоичной системе счисления, где q=2, (используются цифры 0, 1) старшая цифра 1:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 и т. д.
Как видно из примера, что уже третье число в ряду продвинулось на разряд выше, т.е. заняло место (если бы это была десятичная) “десятков”. Пятое число – место “сотен”, девятое число – место “тысяч” и т.д. В десятичной системе переход на другой разряд происходит значительно медленнее. Двоичная система удобна для компьютеров, а для человека неудобна из-за её громоздкости и непривычной записи.
Перевод чисел из десятичной в двоичную систему и наоборот выполняют программы в компьютере. Однако чтобы работать и использовать профессионально компьютер, следует понимать слово машины. Для этого разработаны восьмеричная и шестнадцатеричная системы.
Для того, что бы с лёгкостью оперировать с этими системами, необходимо научится переводить числа из одной системы в другую и наоборот, а так же выполнять простейшие действия над числами - сложение, вычитание, умножение, деление.
1.10 Выполнение арифметических операций в позиционных системах счисления
Правила выполнения основных арифметических операций в десятичной системе хорошо известны – это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицы сложения и умножения для каждой системы получаются свои.
Арифметические действия в позиционных системах счисления выполняются по общим правилам. Необходимо только помнить, что перенос в следующий разряд при сложении и заем из старшего разряда при вычитании определяются величиной основания системы счисления.
При выполнении арифметических действий числа, представленные в разных системах счисления, нужно сначала привести к одному основанию.
Сложение
Таблицы сложения легко составить, используя правило счёта. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево в следующий разряд.
Таблица 1.4
Сложение в двоичной системе:
| + | ||
Таблица 1.5
Сложение в восьмеричной системе
| + | ||||||||
Таблица 1.6
Сложение в шестнадцатеричной системе
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Например:
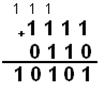
а) Сложим числа 11112 и 1102:
в) Сложим числа F16 и 616:
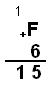
б) Сложим числа 178 и 68:
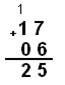
г) Сложим два числа: 178 и 1716.
Приведем число 1716 к основанию 8 посредством двоичной системы
1716=101112=278. Выполним сложение в восьмеричной системе:
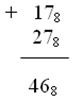
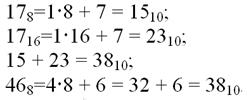
д)Сложим 2 числа. 100001112 + 8910
1 способ: Переведем в десятичную запись число 100001112.
100001112 = 1*27 + 1*22 + 1*21 + 1*20 =128 + 4 + 2 + 1 = 13510
13510 + 8910 = 22410
2 способ: Переведем число 8910 в двоичную систему любым способом.
8910 = 10110012
Сложим эти числа.

Для проверки переведем это число в десятичную запись.
111000002 = 1*27 + 1*26 +1*25 = 128+64+32 = 22410
Вычитание
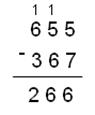
Найдем разность между числами:
а) 6558 и 3678 б) F516 и 616
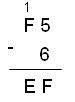
Умножение
Таблица 1.7
Умножение в двоичной системе:
| * | ||
Таблица 1.8
Умножение в восьмеричной системе
| * | ||||||||
Таблица 1.9
Умножение в шестнадцатеричной системе
| * | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| C | F | 1B | 1E | 2A | 2D | |||||||||||
| C | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 4D | 5B | |||||||||||
| A | 1B | 2D | 3F | 5A | 6C | 7E | ||||||||||
| A | A | B | 1E | 3C | 5A | 6E | 8C | |||||||||
| B | B | C | 2C | 4D | 6E | 8F | 9A | A5 | ||||||||
| C | C | D | 3C | 6C | 9C | A8 | B4 | |||||||||
| D | D | E | 1A | 4E | 5B | 8F | 9C | A9 | B6 | C3 | ||||||
| E | E | F | 1C | 2A | 7E | 8C | 9A | A8 | B6 | C4 | D2 | |||||
| F | F | 1E | 2D | 3C | 4B | 5A | A5 | B4 | C3 | D2 | E1 |
Например:
а) Перемножим числа 1012 и 1102

б) Перемножим числа 10А16 и 1A016

Деление
а) Разделим число 111102 на 1102
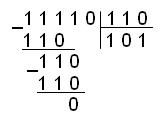
б) Разделим число 133518 на 1638
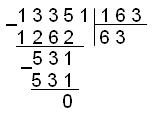
в) Разделим число 3608 на 68
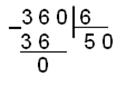
г) Разделим число 1000112 на 11102

1.11 Представление чисел в памяти компьютера
Дата добавления: 2016-04-11; просмотров: 3689;
