Представление вещественных чисел

Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.

Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:

R = m *рⁿ

Например, число 25,324 можно записать в таком виде: 0.25324х10². Здесь m = 0.25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».

Однако справедливы и следующие равенства:

25,324 = 2,5324*10¹ = 0,0025324*10⁴ = 2532,4*10² и т.п.

Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: 0,1_p <= m < 1_p.

Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит, для рассмотренного числа нормализованным представлением будет: 0.25324 * 10².

При работе с числами в языках программирования и вычислительных системах используется экспоненциальная форма записи:

R = m∙E ± n,где Е - десятичное основание системы.

Например: 3,1467890000Е + 2 = 314,6789

1.12 Единицы измерения информации

Напомним, что последовательностью битов можно закодировать текст, изображение, звук или какую-либо другую информацию. Такой метод представления информации называется двоичным кодированием (binary encoding).

В информатике часто используется величина, называемая байтом (byte) и равная 8 битам. И если бит позволяет выбрать один вариант из двух возможных, то байт, соответственно, 1из 256 (2⁸).

В большинстве современных ЭВМ при кодировании каждому символу соответствует своя последовательность из восьми нулей и единиц, т. е. байт. Соответствие байтов и символов задается с помощью таблицы, в которой для каждого кода указывается свой символ.

Наряду с байтами для измерения количества информации используются более крупные единицы:

1 Кбайт (один килобайт) = 2¹⁰ байт = 1024 байта;

1 Мбайт (один мегабайт) = 2¹⁰ Кбайт = 1024 Кбайта=2²⁰ байт;

1 Гбайт (один гигабайт) = 2¹⁰ Мбайт = 1024 Мбайта=2³⁰ байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Тбайт (один терабайт) = 2¹⁰ Гбайт = 1024 Гбайт = 2⁴⁰ байт,

1 Пбайт(один петабайт) = 2¹⁰ Тбайт= 1024 Тбайт = 2⁵⁰ байт.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит = Log₂N), а десятичная (дит) единица информации и измеряется по формуле lgN. Если измерение ведётся в экспоненциальной системе, то единица информации будет нат = lnN .

Например:

а) Книга содержит 100 страниц; на каждой странице - 35 строк, в каждой строке -50 символов. Рассчитаем объем информации, содержащийся в книге.

Т. к. один символ - 1 байт, то страница содержит 35 x 50 = 1 750 байт информации. Объем всей информации в книге (в разных единицах):

1 750 x 100 = 175 000 байт.

175 000 / 1 024 = 170,8984 Кбайт.

170,8984 / 1 024 = 0,166893 Мбайт.

б) Оперативная память компьютера содержит 163 840 машинных слов (наибольшую последовательность бит, которую процессор может обрабатывать как единое целое), что составляет 0,625 Мбайт. Подсчитаем, сколько бит содержит каждое машинное слово?

Переведем 0,625 Мбайт в биты:

0,625 (Мбайт) = 0,625 х 2¹⁰ (Кбайт) = 0,625 х 2¹⁰ х 2¹⁰ (байт)

= 0,625 х 2¹⁰ х 2¹⁰ х 2³(бит) = 0,625 х 2²³ (бит)

=0,625 х 8 388 608 (бит) = 5 242 880 (бит).

Разделим объем оперативной памяти на количество машинных слов: 5 242 880 (бит) / 163 840 (машинных слов) = 32 (бит).

Алгебра логики

2.1. Основные определения алгебры логики

Алгебра логики (булева алгебра)- это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Рассмотрим простой жизненный пример.

Есть настольная лампа, включённая в розетку (Рис. 2.1).

Рис. 2.1. Пример схемы включения настольной лампочки

Для того, что бы лампочка горела (событие F), необходимо совместное соблюдение следующих условий (Рис. 2.2):

«Есть электричество» – высказывание А

«Вилка включена в розетку» – высказывание B

«Выключатель включён» – высказывание C

«Лампочка исправна» – высказывание D

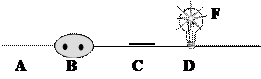
Рис. 2.2.Основные условия горения лампочки

Если высказывания A, B, C, D имеют место (истинны), то лампочка должна гореть, т.е. высказывание F так же имеет место (истинно).

Высказывание «Выключатель включён» на Рис. 2.1. будет иметь значение Ложь, а на Рис. 2.2 Истина.

Высказывание считают атомарнымили элементарным, если оно сообщает единичный факт и никакую его часть нельзя рассматривать как отдельное высказывание.

Например, элементарные высказывания «Трава зеленая» - истинно, а «2*2=5» - ложно.

Высказывания, относящиеся к числу общеизвестных истин, называются трюизмами.

Примером трюизма является высказывание «Волга впадает в Каспийское море».

Зачастую высказывания говорят не о единичном факте, а о целом множестве утверждений. Такие высказывания часто называют общими.

Так высказывания «Большинство членов собрания проголосовало за первое предложение» и «Простых чисел бесконечно много» являются общими.

Сложные высказывания образуются из атомарных применением 3-х видов операций:

1. логические связки ("не", "и", "или", "если... , то", "тогда и только тогда" и другие) применяются к высказываниям и в результате дают новое высказывание, которое называется составным;

2. модальности применяются к высказываниям и изменяют наше отношение к ним;

3. кванторные конструкции применяются к совокупности однородных вычислений либо выражений и дают единое высказывание либо выражение, не зависящее от упомянутых выше параметров.

Например, из элементарных высказываний «Петров — врач», «Петров — шахматист» при помощи связки «и» можно получить составное высказывание «Петров — врач и шахматист», понимаемое как «Петров — врач, хорошо играющий в шахматы».

При помощи связки «или» из этих же высказываний можно получить составное высказывание «Петров — врач или шахматист», понимаемое в алгебре логики как «Петров или врач, или шахматист, или и врач и шахматист одновременно».

Не всякое предложение является логическим высказыванием.

Высказываниями не являются: вопросительные и восклицательные предложения, определения.

Помимо высказываний в естественном языке имеется множество предложений такой же грамматической структуры, которые, тем не менее, принципиально не могут иметь чёткой и однозначной интерпретации. Их называют квазивысказываниями. К ним относятся все оценочные высказывания.

Например, «Саша любит Машу» - квазивысказывание.

Посредством модальностей квазивысказывания неразрывно связаны с высказываниями. Например, «Саша заявил, что любит Машу» - уже высказывание, а «Мне кажется, что Волга впадает в Каспийское море» - квазивысказывание.

Элементарные высказывания на языке алгебры логики обозначаются высказывательскими (пропозициональными) переменными: A, B, C, В и так далее.

Например, если высказывание «Саша изучает логику» обозначить через B, а «Женя изучает логику» - через C, то

«B и C» читается как «Саша и Женя изучают логику»,

«B или C» - «Саша или Женя изучает логику»,

«если B то C» - «Если Саша изучает логику, то Женя тоже изучает логику»,

«B тогда и только тогда, когда C» - «Саша изучает логику тогда и только тогда, когда и Женя изучает логику».

2.2. Основные операции алгебры логики

Соглашение 1. Единственными логическими значениями являются истина и ложь. Истина обозначается как И, или 1, или Т, а ложь обозначается как Л, или 0, или ^.

Как только пытаются предложить другие значения, как, например, «неизвестность», так сразу появляются возражения типа, что степеней неизвестности много и, значит, она сама по себе не является логическим значением.

Соглашение 2. Логическое значение сложного утверждения зависит лишь от логических значений его компонент, а не от смысла.

Соглашение 3. Как только задана интерпретация и зафиксированы значения всех встречающихся в элементарной формуле переменных, становится известно и логическое значение элементарной формулы.

Рассмотрим реализацию базовых логических элементов[6] через электрические контактные схемы, электронные схемы и таблицы истинности[7]. Контакты на схемах будем обозначать латинскими буквами.