Точка приложения силы Архимеда

Автор: Некоторое тело погружено в воду. К какой точке приложена сила Архимеда?

Читатель: Что значит «к какой точке»? Сила Архимеда – это распределенная сила, которая действует на все участки поверхности погруженного в жидкость тела (рис. 29.8).

Автор: Да, но очень удобно представить совокупное действие всех этих распределенных сил как одну силу, приложенную к конкретной точке (если это, конечно, возможно).

Рассмотрим тело, погруженное в жидкость (частично или полностью) (рис. 29.9). Силы давления жидкости действуют только на ту часть тела, которая находится в жидкости.

Заменим тело «куском» затвердевшей жидкости такой же плотности, имеющим форму погруженной в жидкость части тела (рис. 29.10). На этот «кусок» действуют точно те же силы давления со стороны окружающей жидкости, что и на тело. Кроме того, на наш выделенный «кусок» затвердевшей жидкости действует сила тяжести, которую, как мы знаем, можно считать приложенной к центру масс этого «куска». Больше никакие силы на наш «кусок» не действуют (действие сил атмосферного давления мы не учитываем, так как они взаимно компенсируются).

Таким образом, чтобы «кусок» затвердевшей жидкости был в равновесии, результирующая сил давления должна быть приложена так, чтобы выполнялись два условия равновесия:

1) ;

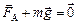2) сумма моментов сил и 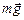равнялась нулю относительно любой точки: М_А + М_mg = 0.

Значит, результирующая сила должна быть направлена вертикально вверх по линии действия силы 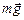(см. рис. 29.10), т.е. по вертикали, проходящей через центр масс вытесненной жидкости.

Таким образом, в качестве точки приложения силы Архимеда годится любая точка на линии действия силы 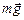. Принято считать, что точкой приложения силы Архимеда является сам центр масс объема жидкости, вытесненной телом. Эту точку называют центром давления жидкости.

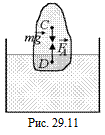
Заметим, что центр давления (точка D), вообще говоря, не совпадает с центром масс плавающего тела (рис. 29.11).

Автор: Ареометр представляет собой запаянную стеклянную трубку, в нижней части которой находится ртуть. Устойчив ли ареометр при погружении в воду к малым отклонениям в сторону?

Читатель: В данном случае центр масс – точка С – из-за большой плотности ртути явно находится ниже центра давления – точки D. Поэтому при малом отклонении от вертикали возникает вращающий момент, который возвращает ареометр в исходное состояние (рис. 29.12). Так что равновесие устойчивое.

Автор: Верно, а вот если точка D будет ниже точки С, то все будет наоборот.

СТОП! Решите самостоятельно: В20.

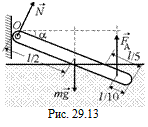
Задача 29.5. Тонкая однородная палочка шарнирно закреплена за верхний конец. Нижний конец палочки погружен в воду. При равновесии под водой находится 1/5 часть длины палочки. Определить плотность вещества палочки. Плотность воды ρ₀.

l/5 ρ0	Решение. Запишем уравнение моментов для палочки относительно оси, проходящей через точку О (рис. 29.13): ,
ρ = ?

где l – длина палочки; a – угол между палочкой и горизонтальной плоскостью; т – масса палочки. Учитывая, что 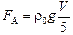, Vρ = т, где ρ₀ – плотность воды; ρ – плотность палочки; V – объем палочки, получаем

.

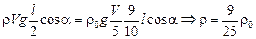Ответ: .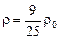

СТОП! Решите самостоятельно: А4, В21, С18, С19.