Работа при погружении тела
Задача 29.6. Плоская льдина площадью S плавает в воде. Какую работу надо совершить внешней силой, чтобы утопить льдину? Высота льдины, выступающая над водой равна h. Плотность воды ρ0.
| S h ρ0 | 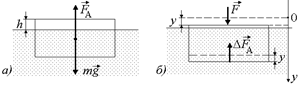 Рис. 29.14
Рис. 29.14
|
| А = ? | |
Решение. Когда льдина свободно плавает, сила тяжести 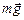 уравновешена силой Архимеда
уравновешена силой Архимеда  (рис. 29.14,а). Если попытаться утопить льдину, прикладывая сверху силу
(рис. 29.14,а). Если попытаться утопить льдину, прикладывая сверху силу 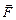 , то льдина начнет погружаться в воду, объем вытесненной телом жидкости увеличится, а значит, возрастает и сила Архимеда. Будем топить льдину медленно так, чтобы ее скорость все время была постоянной, а сумма всех действующих на нее сил равнялась нулю.
, то льдина начнет погружаться в воду, объем вытесненной телом жидкости увеличится, а значит, возрастает и сила Архимеда. Будем топить льдину медленно так, чтобы ее скорость все время была постоянной, а сумма всех действующих на нее сил равнялась нулю.
Рассмотрим ситуацию, когда льдина погрузилась по сравнению с исходным положением на глубину у (рис. 29.14,б). При этом сила Архимеда возросла по сравнению с первоначальным значением на 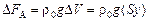 . Чтобы сумма сил, приложенных к льдине, при этом по-прежнему оставалась равной нулю, необходимо, чтобы «утапливающаяся» сила F равнялась точно такой же величине: F = =DFA = ρ0gSy.
. Чтобы сумма сил, приложенных к льдине, при этом по-прежнему оставалась равной нулю, необходимо, чтобы «утапливающаяся» сила F равнялась точно такой же величине: F = =DFA = ρ0gSy.
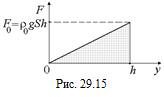 Построим график зависимости F = F(y) (рис. 29.15). При у = 0 F = 0, при y = h F0 = ρ0gSh, 0 < y < h. Работа этой силы численно равна площади под графиком F(y):
Построим график зависимости F = F(y) (рис. 29.15). При у = 0 F = 0, при y = h F0 = ρ0gSh, 0 < y < h. Работа этой силы численно равна площади под графиком F(y):
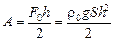 .
.
Ответ: 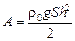 .
.
СТОП! Решите самостоятельно: В22, В23, С21.
Задача 29.7. Тело массой т всплывает в жидкости плотностью ρж на высоту h. Какую скорость будет иметь тело, если объем тела V, а трения нет?
| m h V ρж | Решение. Применим к нашему телу теорему о кинетической энергии (ТКЭ): К2 – К1 = Аmg + АА, где 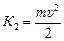 ; К1 = 0; Amg = –mgh; AA = ρжVgh. Тогда ; К1 = 0; Amg = –mgh; AA = ρжVgh. Тогда
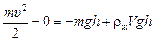 .
Отсюда .
Отсюда
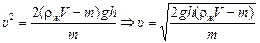 .
Ответ: .
Ответ: 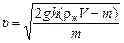 . .
|
| υ = ? | |
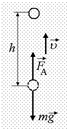 Рис. 29.16
Рис. 29.16
|
СТОП! Решите самостоятельно: В25, С22, С23.
Дата добавления: 2016-04-11; просмотров: 2713;
