Равнопеременное движение тела
Движение по данной траектории называется равнопеременным, если среднее ускорение по направлению 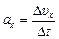 одно и то же за любой промежуток времени Dt.
одно и то же за любой промежуток времени Dt.
Пусть тело движется равнопеременно по направлению х с ускорением ах = const. Пусть в момент времени t0 скорость по направлению равна υх0. Тогда скорость по направлению в произвольный момент времени t будет равна
υх(t) = υх0 + ах(t – t0). (5.6)
Задача 5.3. По графикам зависимостей ах = ах(t) (рис. 5.5) определить Dυх за время Dt и значение υх(t1), если υх(t0) = υх0.
| Dt υх0 ax0 | 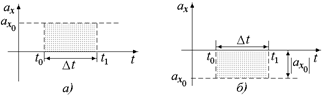 Рис. 5.5
Рис. 5.5
|
| Dυх = ? υх(t1) = ? | |
Решение.
1. На рис. 5.5,а, с одной стороны, движение равнопеременное, ах0 > 0, Dυх = ах0Dt > 0. С другой стороны, получаем, что Dυх можно вычислить как площадь заштрихованного прямоугольника под графиком ах(t) со сторонами ах0 и Dt. Тогда υх(t1) = υх0 + Dυх = υх0 + ах0Dt.
2. На рис. 5.5,б, с одной стороны, движение равнопеременное, ах0 < 0, Dυх = ах0Dt < 0. С другой стороны, получаем, Dυх = –| ах0|Dt < 0, т.е. Dυх можно посчитать как минус площадь заштрихованного прямоугольника над графиком ах(t) со сторонами |ах0| и Dt. Тогда υх(t1) = = υх0 + ах0Dt.
Из решения задачи следует важный вывод: площадь под графиком ах(t) на участке Dt равна Dυх > 0 за время Dt; площадь над графиком ах(t) на участке Dt равна –Dυх за время Dt, где Dυх < 0.
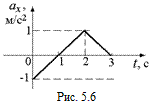 Задача 5.4. Дан график зависимости ах = ах(t) (рис. 5.6). Известно, что υх(0) = = –2 м/с. Определите значения υх(t) в моменты времени: t1 = 1 с, t2 = 2 с, t3 = 3с.
Задача 5.4. Дан график зависимости ах = ах(t) (рис. 5.6). Известно, что υх(0) = = –2 м/с. Определите значения υх(t) в моменты времени: t1 = 1 с, t2 = 2 с, t3 = 3с.
Решение.
1. На участке (0; 1) изменение проекции скорости Dυх1 равно площади над графиком ах(t), взятой со знаком "минус": Dυх1 = –0,5 м/с. Тогда υх(1) = υх(0) + Dυх1 = (–2 м/с) + (–0,5 м/с) = –2,5 м/с.
2. На участке (1; 2) изменение проекции скорости Dυх2 равно площади под графиком ах(t), взятой со знаком "плюс": Dυх2 = 0,5 м/с. Тогда υх(2) = υх(1) + Dυх2 =(–2,5 м/с) + 0,5 м/с = –2 м/с.
3. На участке (2; 3) изменение проекции скорости Dυх3 равно площади под графиком ах(t), взятой со знаком "плюс": Dυх3 = 0,5 м/с. Тогда υх(3) = υх(2) + Dυх3 =(–2 м/с) + 0,5 м/с = –1,5 м/с.
Ответ: υх(1) = –2,5 м/с, υх(2) = –2 м/с, υх(3) = –1,5 м/с.
СТОП! Решите самостоятельно: В5 (а), В6 (а,б), В8, С1.
Пусть тело движется равнопеременно и пусть в начальный момент мгновенная скорость по направлению равна  , а в конечный момент
, а в конечный момент 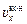 . Тогда средняя скорость по направлению за данный промежуток времени равна:
. Тогда средняя скорость по направлению за данный промежуток времени равна:
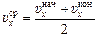 . (5.7)
. (5.7)
Докажем эту формулу.
1. Рассмотрим случай, когда  > 0 и
> 0 и 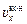 > 0. Тогда скорости по направлению равны путевым скоростям:
> 0. Тогда скорости по направлению равны путевым скоростям:  = υнач,
= υнач, 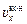 = υкон, движение является либо равноускоренным, либо равнозамедленным, а
= υкон, движение является либо равноускоренным, либо равнозамедленным, а 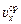 = υср. Отсюда согласно формуле (5.2)
= υср. Отсюда согласно формуле (5.2)
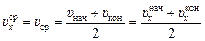
что и требовалось доказать.
2. Рассмотрим случай, когда  < 0 и
< 0 и 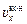 < 0. Тогда
< 0. Тогда  = = –υнач,
= = –υнач, 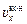 = –υкон, движение является либо равноускоренным |
= –υкон, движение является либо равноускоренным | 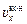 | > |
| > |  |, либо равнозамедленным |
|, либо равнозамедленным | 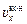 | < |
| < |  |. Отсюда справедливо
|. Отсюда справедливо
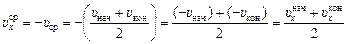 ,
,
что и требовалось доказать.
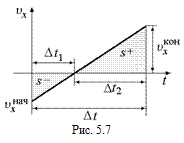 3. Рассмотрим случай, когда в процессе движения υх(t) меняет знак. Пусть
3. Рассмотрим случай, когда в процессе движения υх(t) меняет знак. Пусть  < 0 и
< 0 и 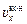 > 0 (рис. 5.7). Тогда
> 0 (рис. 5.7). Тогда 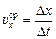 ,
,
Dх = s+ – s– =
=  . (1)
. (1)
Пусть ах – ускорение по направлению, тогда
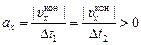 Þ
Þ
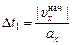 ,
, 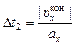 .
.
Подставим значения Dt1 и Dt2 в (1) и получим
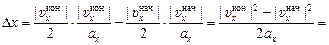
= 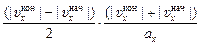 ,
,
 ,
,
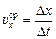 =
= 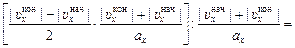
= 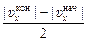 .
.
Поскольку  ,
, 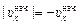 , то
, то 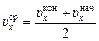 , что и требовалось доказать.
, что и требовалось доказать.
Случай  > 0 и
> 0 и 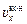 < 0 доказывается аналогично.
< 0 доказывается аналогично.
Задача 5.5.Тело брошено вертикально вверх со скоростью υ0 = = 19,6 м/с. На какой высоте от земли будет находиться тело через t = 3 с, если известно, что скорость тела в этот момент равна υ1 = = 9,8 м/с и направлена вниз? Движение считать равнопеременным.
| υ0 = 19,6 м/с υ1 = 9,8 м/с t = 3 с | Решение. Направим ось х вверх (рис. 5.8).
Пусть тело было брошено из точки с координатой х = 0. Тогда  = + υ0, = + υ0, 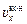 = –υ1. Отсюда = –υ1. Отсюда
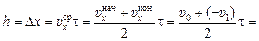
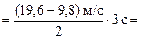 14,7 м.
Ответ: 14,7 м.
Ответ: 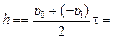 14,7 м.
СТОП! Решите самостоятельно: С4–С6. 14,7 м.
СТОП! Решите самостоятельно: С4–С6.
|
| h = ? | |
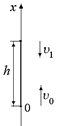 Рис. 5.8
Рис. 5.8
|
Дата добавления: 2016-04-11; просмотров: 1030;
