Как по графику зависимости координаты

от времени х = х(t) построить график

зависимости пути от времени s = s(t)?

Отметим следующие особенности графика s = s(t):

1) график s = s(t) всегда начинается из начала координат, так как в начальный момент пройденный путь всегда равен нулю;

2) график s = s(t) всегда не убывает: он либо возрастает, если тело движется, либо не меняется, если тело стоит;

3) функция s = s(t) нe может принимать отрицательное значение.

Из сказанного следует, что график х = х (t) совпадает с графиком s = s(t) только в том случае, если х(0) = 0 и x(t) все время не убывает, т.е. тело движется только в положительном направлении либо стоит на месте.

Приведем несколько примеров построения графиков s = s(t) по данным графикам х = х(t).

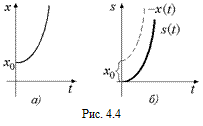Пример 4.2.По графику х = = х(t) на рис. 4.4,а построить график s = s(t).

График х = х(t) возрастает, но начинается не в начале координат, а в точке (0, х₀). Для того чтобы получить график s = s(t) необходимо опустить график х = х(t) на x₀ вниз (рис. 4.4,б).

Пример 4.3.По графику х = х(t) на рис. 4.5,а построить график s = s(t).

В данном случае х(0) = 0, но тело движется в отрицательном направлении оси х. В данном случае справедливо s(t) = |x(t)|, и для построения графика s = s(t) достаточно отобразить график х = х(t) зеркально на верхнюю полуплоскость (рис. 4.5,б).

Рис. 4.5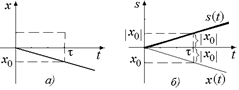

Пример 4.4.По графику х = х(t) на рис. 4.6,а построить график s = s(t).

Сначала опустим график х = х(t) на х₀ вниз, чтобы х(0) = 0, как мы это делали в примере 4.2, а затем прямую 2 (рис. 4.6,б) зеркально отобразим на верхнюю полуплоскость, как мы это сделали в примере 4.3.

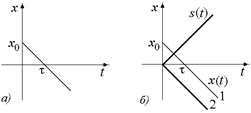Рис. 4.6

Пример 4.5.По графику х = х(t) на рис. 4.7,а построить график s = s(t).

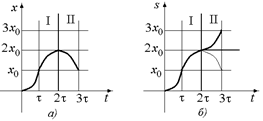Рис. 4.7

График х = х(t) состоит из двух участков: на первом участке [0; 2t] х(t) воз­растает, а на втором участке [2t; 3t] – убывает, т.е. тело движется в отрицательном направлении оси х. Поэтому для построения графика s = s(t) первую часть графика х = х(t) мы оставляем без изменения, а вторую часть зеркально отражаем относительно прямой, проходящей через точку поворота (2t, 2х₀) параллельно оси t (рис. 4.7,б).

СТОП! Решите самостоятельно: С2 (а, б, в).

Утверждение. Пусть дан график зави­симости υ_х(t), х(t₁) = x₀ (рис. 4.8). Значения площадей над графиком s⁺ и под гра­фиком s^–, выраженные с учетом масшта­бов в единицах длины, известны. Тогда путь, пройденный за промежуток времени [t₁, t₂], равен:

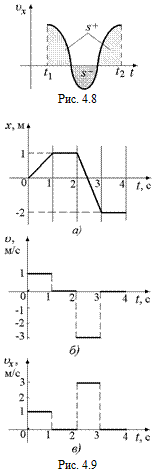s = s^–+ s⁺. (4.2)

Координата в момент времени t₂ равна:

х(t₂) = x₀ – s^–+ s⁺. (4.3)

Задача 4.2. По графику зави­симости координаты от времени (рис. 4.9,а) построить графики зависимостей υ_х = υ_х(t) и υ = υ (t).

Решение. Рассмотрим промежуток времени [0; 1]. На этом промежутке Dх = = 1 м, Dt = 1 с, отсюда 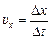= 1 м/с, υ = = |υ_х| = 1 м/с.

Рассмотрим промежуток времени [1; 2]. На этом промежутке Dх = 0, значит, υ_х = υ = 0.

Рассмотрим промежуток времени [2; 3]. На этом промежутке Dх = (–2) – 1 = = –3 м, Dt = 1 с, значит, 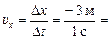= –3 м/с, υ = |υ_х| = 3 м/с.

Рассмотрим промежуток времени [3; 4]. На этом промежутке Dх = 0, следовательно, υ_х = υ = 0.

Графики приведены на рис. 4.9,б и 4.9,в.

СТОП! Решите самостоятельно: В3 (а,б,в).

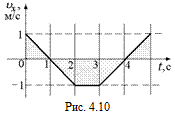Задача 4.3. По графику зависимости υ_х = υ_х(t) (рис. 4.10) найти значения пройденного пути и координаты в моменты времени 1c, 2 с, 3 с, 4 с, 5 с, если х(0) = 2,0 м.

Решение.

1. Рассмотрим промежуток времени [0; 1]. На этом промежутке υ_х(t) убывала от 1 м/с до 0, т.е. тело двигалось вдоль оси х замедленно и в момент t = 1 с остановилось. Пройденный путь равен площади под графиком на участке [0, 1]: 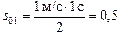м. Координата в момент t = 1 с равна х(1) = х(0) + s₀₁ = 2,0 м + 0,5 м = 2,5 м.

2. Рассмотрим промежуток времени [1; 2]. На этом промежутке υ_х уменьшалась от 0 до –1 м/с, т.е. тело разгонялось из состояния покоя в направлении, противоположном направлению оси х. Путь, пройденный за этот промежуток вре­мени, равен площади над графиком υ_х = υ_х(t) на промежутке [1; 2]: 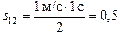м. Следовательно, общий путь, пройденный телом в момент t = 2 с, равен s(2) = s(1) + s₁₂ = 0,5 м + 0,5 м = 1,0 м. Координата в момент t = 1 с равна х(2) = х(1) – s₁₂ = 2,5 м – 0,5 м = 2,0 м.

3. Рассмотрим промежуток времени [2; 3]. На этом промежутке тело движется равномерно в отрицательном направлении оси х с путевой скоростью υ = 1 м/с. Пройденный путь равен s₂₃ = (1 м/с)´ ´(1 с) = 1,0 м. Следовательно, путь, пройденный к моменту t = 3 с, равен s(3) = s(2) + s₂₃ = 1,0 м + 1,0 м = 2,0 м.

Координата же за этот промежуток времени уменьшалась на величину пройденного пути, так как тело двигалось в обратную сторону: х(3) = х(2) – s₂₃ = 2,0 м – 1,0 м = 1,0 м.

4. Рассмотрим промежуток времени [3; 4]. На этом промежутке тело продолжало двигаться в отрицательном направлении, но путевая скорость уменьшалась от 1 м/с до нуля, т.е. в момент t = 4 с тело остановилось. Пройденный путь равен площади над графиком на участке [3; 4]: 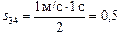м. Путь, пройденный к моменту t = 4 с, равен s(4) = s(3) + s₃₄ = 2,0 м + 0,5 м = 2,5 м.

Координата уменьшилась на величину s₃₄: х(4) = х(3) – s₃₄ = = 1,0 м – 0,5 м = 0,5 м.

5. Рассмотрим, промежуток времени [4; 5]. На этом промежутке тело двигалось в положительном направлении оси х, путевая скорость тела при этом возрас­тала от нуля до 1 м/с. Путь, пройденный телом за промежуток времени [4; 5], равен: 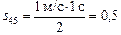м. Общий путь, пройденный к моменту t = 5 c, s(5) = s(4) + s₄₅ = 2,5 м + 0,5 м = 3 м.

Координата увеличилась на величину пути s₄₅ = 0,5 м и стала равна: х(5)= х(4) + s₄₅ = 0,5 м + 0,5 м = 1 м.

Ответ: s(1) = 0,5 м, s(2) = 1 м, s(3) = 2 м, s(4) = 2,5 м, s(5) = 3 м;

х(1) = 2,5 м, х(2) = 2 м, х(3) = 1 м, х(4) = 0,5 м, х(5) = 1 м;

СТОП! Решите самостоятельно: С3 (а, б, в).