Ускорение. ускорение по направлению
Средним путевым ускорением называется величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:
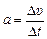 . (5.1)
. (5.1)
Мгновенным путевым ускорением называется величина, равная отношению: 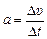 при Dt ®0, где Dυ – изменение мгновенной путевой скорости, а Dt – промежуток времени, в течение которого это изменение произошло.
при Dt ®0, где Dυ – изменение мгновенной путевой скорости, а Dt – промежуток времени, в течение которого это изменение произошло.
Если тело движется так, что его мгновенное путевое ускорение положительно: а > 0, то такое движение называется ускоренным.
Если тело движется так, что его мгновенное путевое ускорение отрицательно: а < 0, то такое движение называется замедленным.
Ускоренное движение называется равноускоренным, если среднее путевое ускорение 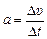 одинаково за любой промежуток времени Dt.
одинаково за любой промежуток времени Dt.
Замедленное движение называется равнозамедленным, если среднее путевое ускорение 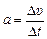 одинаково за любой промежуток времени Dt.
одинаково за любой промежуток времени Dt.
Задача 5.1.По графику зависимости а = а(t) (рис. 5.1) определить, в какие промежутки времени тело двигалось: а) ускоренно; б) замедленно. Направление движения не менялось.
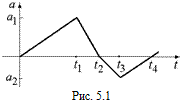 Решение. На участке (0; t2) ускорение положительно, значит, скорость тела увеличивается.
Решение. На участке (0; t2) ускорение положительно, значит, скорость тела увеличивается.
На участке (t2; t4) ускорение отрицательно, значит, скорость тела уменьшается.
Следовательно, на участке (0; t2) движение ускоренное, на участке (t2; t4) движение замедленное. Наибольшее значение скорость достигает в момент времени t2.
СТОП! Решите самостоятельно: А1, А2.
Пусть тело движется равноускоренно или равнозамедленно и пусть начальная скорость тела равна υн, а конечная υк, тогда средняя путевая скорость тела за данное время равна:
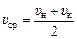 . (5.2)
. (5.2)
Докажем эту формулу. Рассмотрим на рис. 5.2 графики зависимостей равноускоренного (а) и равнозамедленного (б) движений.
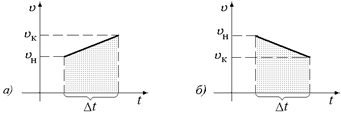
Рис. 5.2
В обоих случаях площадь под графиком υ(t) представляет собой трапецию с основаниями υнач и υкон и высотой Dt. Пройденный путь можно вычислить как площадь под графиком 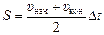 , где Dt – время движения. Тогда
, где Dt – время движения. Тогда 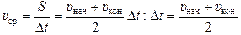 , что и требовалось доказать.
, что и требовалось доказать.
СТОП! Решите самостоятельно: В1, В2.
Средней проекцией ускорения на данное направление или среднимускорением по направлению за время Dt называется величина, равная отношению изменения проекции скорости Dυх ко времени Dt, за которое это изменение произошло:
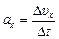 . (5.3)
. (5.3)
Мгновеннойпроекцией ускорения на данное направление или мгновенным ускорением по направлению называется величина, равная:
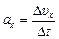 при Dt ®0, (5.4)
при Dt ®0, (5.4)
где Dυх – изменение мгновенной скорости по направлению за время Dt.
Автор: Как Вы считаете, справедливо ли равенство а = ах?
Читатель: Я думаю, что нет. Пусть, например,  = 0, а
= 0, а  = = –1 м/с и Dt = 1 с. Тогда
= = –1 м/с и Dt = 1 с. Тогда  –1 м/с2, а
–1 м/с2, а  1 м/с2. Видимо, верно а = |ax| .
1 м/с2. Видимо, верно а = |ax| .
Автор: Это утверждение также неверно. Пусть, например,  = 0, а
= 0, а  = 10 м/с, Dt = 10 с. Тогда
= 10 м/с, Dt = 10 с. Тогда
 –1 м/с2;
–1 м/с2;
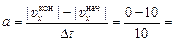 –1 м/с2.
–1 м/с2.
Ясно, что |ax| = |–1 м/c2| = 1 м/с2 ¹ а = –1 м/с2!
Разберемся с этим вопросом подробно.
1. Пусть тело движется в положительном направлении по оси х, тогда υх > 0,  = υнач,
= υнач,  = υкон, отсюда
= υкон, отсюда
Dυх =  –
–  = υкон – υнач = Dυ Þ ах = а.
= υкон – υнач = Dυ Þ ах = а.
2. Пусть тело движется в отрицательном направлении по оси х, тогда υх < 0,  = –υнач,
= –υнач,  = –υкон, отсюда
= –υкон, отсюда
Dυх =  –
–  = –υкон – (–υнач) = –(υкон – υнач) = –Dυ Þ ах = –а.
= –υкон – (–υнач) = –(υкон – υнач) = –Dυ Þ ах = –а.
Отсюда вытекает, что справедливо соотношение:
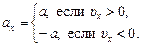 (5.5)
(5.5)
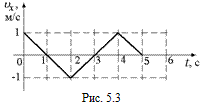
Задача 5.2.По данному графику зависимости проекции скорости от времени (рис. 5.3) постройте графики зависимостей проекции ускорения от времени ах = ах(t) и путевого ускорения от времени а = а(t).
Решение.
1. Сначала вычислим значения ах на каждом из промежутков времени: (0; 2), (2; 4), (4; 5). В пределах каждого из этих промежутков наклон графика υх(t) не меняется, поэтому в пределах каждого из этих промежутков ах – величина постоянная.
 Промежуток (0; 2):
Промежуток (0; 2):
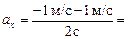 –1 м/с2.
–1 м/с2.
Промежуток (2; 4):
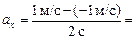 1 м/с2.
1 м/с2.
Промежуток (4; 5): 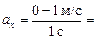 –1 м/с2.
–1 м/с2.
Теперь по формуле (5.2) вычислим значения а для каждого из временных интервалов: (0; 1), (1; 2), (2; 3), (3; 4), (4;5).
Промежуток (0; 1): υх > 0 а = ах = –1м/с2.
Промежуток (1; 2): υх < 0 а = –ах = –(–1 м/с2) = 1 м/с2.
Промежуток (2; 3): υх < 0 а = –ах = –1м/с2.
Промежуток (3; 4): υх > 0 а = ах = 1м/с2.
Промежуток (4; 5): υх > 0 а = ах = –1м/с2.
Графики зависимости ах(t) и a(t) представлены на рис. 5.4.
Рис. 5.4 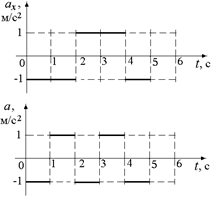
СТОП! Решите самостоятельно: В3, В4, С3.
Дата добавления: 2016-04-11; просмотров: 2953;
