Основное уравнение равнопеременного движения
Пусть материальная точка движется по заданной траектории равнопеременно. Известно, что ах = const, υх(t0) = υ0х, х(t0) = х0. Тогда в момент времени t координата х(t) будет равна
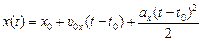 . (6.1)
. (6.1)
Доказательство.
x(t) = x0 + Dx,
где
Dx = 
= 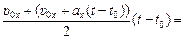
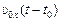
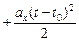 .
.
Отсюда 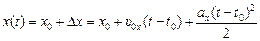 , что и требовалось доказать.
, что и требовалось доказать.
Частные случаи:
1) если t0 = 0, то
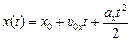 ; (6.2)
; (6.2)
2) если t0 = 0 и х0 = 0, то
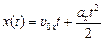 ; (6.3)
; (6.3)
3) если t0 = 0, х0 = 0 и υ0х = 0, то
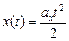 ; (6.4)
; (6.4)
4) если направление движения не меняется, то путь, пройденный телом за время t, равен s = x(t) – x0, т.е.
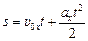 . (6.5)
. (6.5)
Задача 6.1.Тело, двигаясь равноускоренно, за первые t1 = 5 с своего движения прошло путь l1 = 100 м, а за первые t2 =10 с своего движения прошло путь l2 = 300 м. Определите начальную скорость тела.
| t1 = 5 с t2 = 10 с l1 = 100 м l2 = 300 м | Решение. Согласно формуле (6.2) имеем:
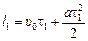 ; (1) ; (1)
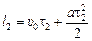 , (2) , (2)
|
| υ0 = ? | |
где а – путевое ускорение, a υ0 – начальная путевая скорость.
Выразим а из уравнения (1): 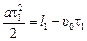 ,
, 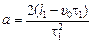 . Подставим значение а в уравнение (2), получим:
. Подставим значение а в уравнение (2), получим:
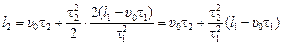 ,
,
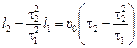 .
.
Из последнего равенства получим значение υ0:
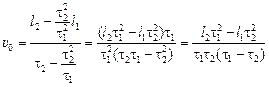 .
.
Подставим численные значения:
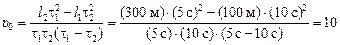 м/с.
м/с.
Ответ: 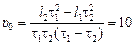 м/с.
м/с.
Стоп! Решите самостоятельно: А2, В1, В2, С1, С14.
Задача 6.2.Машинист пассажирского поезда, двигавшегося со скоростью υ1 = 108 км/ч, заметил на расстоянии l0 = 180 м впереди движущийся в ту же сторону со скоростью υ2 = 32,4 км/ч товарный поезд. Машинист сразу же начал торможение с ускорением, по модулю равным |а| =1,2 м/с2. Достаточно ли этого для того, чтобы поезда не столкнулись? Если столкновение произойдет, то через какое время?
| υ1 = 108 км/ч = 30,0 м/с υ2 = 32,4 км/ч = 9,00 м/с l0 = 180 м |а| =1,2 м/с2 | Решение. 1. Так как пассажирский поезд движется равнозамедленно, то aх = –|а|. 2. Пусть x1 – координата локомотива пассажирского поезда, а х2 – координата |
| tв = ? |
конца последнего вагона товарного поезда. Тогда, считая t0 = 0, согласно формуле (6.3) можем записать уравнения:
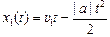 ;
; 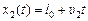 .
.
Условие столкновения: 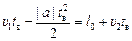 . Преобразуем это уравнение:
. Преобразуем это уравнение: 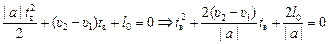 .
.
Решим данное квадратное уравнение относительно искомой величины tв:
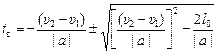 .
.
Подставим численные значения:
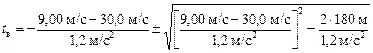 ,
,
tв1 » 15 с, tв2 » 20 с.
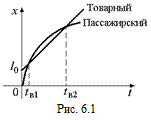 Что означают два значения tв? Если бы поезда шли по параллельным путям, то передняя точка локомотива пассажирского поезда и задняя точка последнего вагона товарного поезда встретились бы дважды: сначала пассажирский поезд (через tв1 = 15 с) обогнал бы последний вагон товарного поезда, а затем (в момент tв2 = = 20 с) товарный поезд обогнал бы пассажирский. Следовательно, столкновения избежать не удастся и произойдет оно через tв = 15 с после начала торможения.
Что означают два значения tв? Если бы поезда шли по параллельным путям, то передняя точка локомотива пассажирского поезда и задняя точка последнего вагона товарного поезда встретились бы дважды: сначала пассажирский поезд (через tв1 = 15 с) обогнал бы последний вагон товарного поезда, а затем (в момент tв2 = = 20 с) товарный поезд обогнал бы пассажирский. Следовательно, столкновения избежать не удастся и произойдет оно через tв = 15 с после начала торможения.
На рис. 6.1 представлен примерный график зависимостей координат товарного и пассажирского поезда от времени.
Ответ:
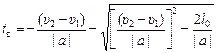 = 15 с.
= 15 с.
СТОП! Решите самостоятельно: А1, В5, В6, С3.
Задача 6.3.Закон нечетных чисел. Тело движется равноускоренно без начальной скорости. За первую секунду тело прошло путь s1 = 1 м. Какой путь пройдет тело за 33-ю секунду своего движения?
| s1 = 1 м t1 = 1 с п = 33 υ0 = 0 | Решение. Пусть а – путевое ускорение тела. Вычислим путь, который тело пройдет за п-ю секунду движения. Этот путь равен разности между путем, пройденным за первые п секунд движения, и путем, пройденным за (п – 1) секунд движения: sп = sпройденный за п с – sпройденный за (п – 1) с, |
| s33 = ? | |
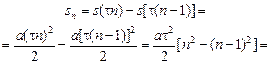
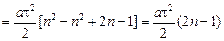 .
.
Итак,
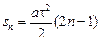 . (1)
. (1)
За первую секунду тело прошло путь  . Подставляя значение s1 в формулу (1), получим:
. Подставляя значение s1 в формулу (1), получим:
sn = s1(2n – 1). (6.6)
Формула (6.6) получила название Закона нечетных чисел.
Вернемся к нашей задаче. Подставим в формулу (6.6) значения п = 33, получим:
sn = s1(2×33 – 1) = s1 × 65 = (1 м) × 65 = 65 м.
Ответ: sn = s1(2n – 1) = 65 м.
СТОП! Решите самостоятельно: А3, В7, В9, С9.
Задача 6.4.Тело начинает двигаться из точки О вверх по наклонной плоскости с начальной скоростью υ0 = 2 м/с. Какой путь прошло тело за время t = 3 с? Движение равнопеременное, ускорение по модулю равно |a| = 1 м/с2.
| υ0 = 2 м/с t = 3 с |a| = 1 м/с2 | Решение. Пусть ось х направлена вверх по наклонной плоскости, тогда υх0 = + υ0 = 2 м/с, а = –|а| = –1 м/с2. |
| s = ? | |
Читатель: Наверное, мы можем в данном случае вычислить путь по формуле (6.5):
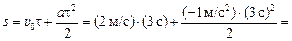 1,5 м.
1,5 м.
Автор:Эта формула справедлива только в том случае, если направление движения не меняется. А так ли это?
В момент остановки скорость равна нулю. Пусть tост – время остановки тела, тогда согласно формуле (5.6) 0 = υ0 + atост, отсюда
tост = – υ0/а = –(2 м/с) : (–1 м/с2) = 2 с.
 По условию задачи время движения t = 3 с > 2 с. Это значит, что, достигнув за 2 с верхней точки своего движения, тело остановилось, а затем в течение еще 1 с двигалось в обратном направлении (рис. 6.2).
По условию задачи время движения t = 3 с > 2 с. Это значит, что, достигнув за 2 с верхней точки своего движения, тело остановилось, а затем в течение еще 1 с двигалось в обратном направлении (рис. 6.2).
Пусть хmax – координата точки поворота тела, xк – конечная координата, а l = (xmax – xк) – путь, пройденный телом в обратном направлении, тогда общий путь, пройденный телом, равен
s = xmax + l = xmax + (xmax – xк) = 2xmax – хк. (1)
Для вычисления xmax и xк воспользуемся формулой (6.3). В нашем случае х0 = 0 и t0 = 0, тогда
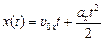 , (2)
, (2)
где υ0х = +υ0, ах = –а.
Подставив в формулу (2) время tост, получим xmах, а подставив t, получим хк. Тогда согласно формуле (1) получим:
s = 2xmax – хк = 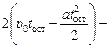
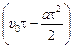 .
.
Подставим численные значения:
s = 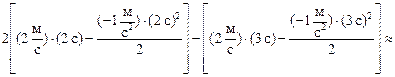
» 2,5 м.
Ответ: s » 2,5 м.
СТОП! Решите самостоятельно: С10–С12.
Связь между координатой,
Дата добавления: 2016-04-11; просмотров: 1401;
