Скоростью и ускорением
Если тело движется равнопеременно и проекция его ускорения ах, начальная скорость υхнач, конечная скорость υхкон, начальная координата хнач, а конечная координата хкон, то справедлива формула
 . (6.7)
. (6.7)
Доказательство.
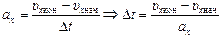 , (1)
, (1)
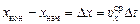 , (2)
, (2)
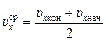 . (3)
. (3)
Подставим Dt из (1) и 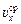 из (3) в (2) и получим
из (3) в (2) и получим

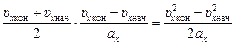 ,
,
что и требовалось доказать.
Частные случаи:
1) при равноускоренном движении а = ах > 0, υхкон = υ > 0, υхнач = υ0 > 0, хкон – хнач = s, тогда путь равен
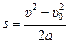 ; (6.8)
; (6.8)
2) при равнозамедленном движении а = –|ах| < 0, υхкон = υ, υхнач = υ0, тогда путь равен
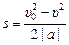 ; (6.9)
; (6.9)
3) если при равнозамедленном движении υ = 0, то
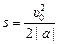 . (6.10)
. (6.10)
Задача 6.5.Поезд начинает движение из состояния покоя и, двигаясь равноускоренно, увеличивает свою скорость. На первом километре скорость возросла на 10 м/с. На сколько возрастет она на втором километре?
| s1 = s2 = s = 1 км Dυ1 = 10 м/с υ0 = 0 | Решение. Пусть поезд движется с путевым ускорением а, υ1 – скорость в конце первого километра, υ2 – в конце 2-го. Тогда согласно формуле (6.8):
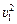 = 2as, (1) = 2as, (1)
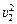 – – 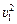 = 2as, (2)
Dυ2 = υ2 – υ1, (3)
Dυ1 = υ1 – 0 = υ1. (4) = 2as, (2)
Dυ2 = υ2 – υ1, (3)
Dυ1 = υ1 – 0 = υ1. (4)
|
| Dυ2 = ? | |
Приравняем левые части равенств (1) и (2), получим 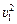 =
= 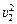 –
– 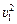 , отсюда
, отсюда 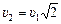 . Подставим значение υ2 в уравнение (3):
. Подставим значение υ2 в уравнение (3):
Dυ2 = 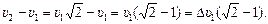
Подставим численные значения:
Dυ2 = 10 м/с ×(  – 1) » 4,1 м/с.
– 1) » 4,1 м/с.
Ответ: Dυ2 = 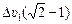 » 4,1 м/с.
» 4,1 м/с.
СТОП! Решите самостоятельно: А4, В10, В11, В15.
Дата добавления: 2016-04-11; просмотров: 692;
