Задачи средней трудности. В1. Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см

В1. Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см. Какой путь он пройдет за 3 с?

В2. При равномерно ускоренном движении точка проходит в первые два равных последовательных промежутка времени, по t = 4,0 с каждый, пути s₁ = 24 м и s₂ = 64 м. Определить начальную скорость и ускорение движущейся точки.

В3. Движения двух мотоциклистов заданы уравнениями х₁ = 15 + t² и х₂ = 8t. Описать движение каждого мотоциклиста, найти время и место их встречи.

В4. В момент начала наблюдения расстояние между двумя телами равно 6,9 м. Первое тело движется из состояния покоя с ускорением 0,20 м/с². Второе движется вслед за ним, имея начальную скорость 2 м/с и ускорение 0,40 м/с². Написать уравнения х = x(t) в системе отсчета, в которой при t = 0 ко­ординаты тел принимают значения, соответственно равные x₁ = 6,9 м, х₂ = 0. Найти время и место встречи тел.

В5.Спустя 40 с после отхода теплохода вдогонку за ним был послан глиссер, который, отправившись от пристани, двигался все время с ускорением 0,50 м/с². Через какое время и на каком рас­стоянии от пристани глиссер догонит теплоход, если теплоход дви­жется равномерно со скоростью 18 км/ч? Начертить на одних осях графики скорости теплохода и глиссера.

В6.Движения двух автомобилей по шоссе заданы уравне­ниями x₁ = = 2t + 0,2t² и x₂ = 80 – 4t. Описать картину движения. Найти: а) время и место встречи автомобилей; б) рас­стояние между ними через 5 с от начала отсчета времени; в) координату первого автомобиля в тот момент времени, когда второй находился в начале отсчета.

В7. Тело движется с постоянным ускорением прямолинейно и в шестую секунду проходит 12 м. Определить ускорение и путь, пройденный в шестнадцатую секунду, если начальная скорость была равна нулю.

В8. Шарик начинает движение по наклонному желобу из состоя­ния покоя с постоянным ускорением 2 см/с². Определить модули пере­мещений за 1, 2 и 3 с, а также за первую, вторую и третью секунды. Каково отношение перемещений в каждом из этиx двух случаев?

В9.Тело, начальная скорость которого была равна нулю, прошло за первую секунду 1 м, за вторую – 2 м, за третью – 3 м, за четвер­тую – 4 м и т.д. Является ли такое движение равноускоренным?

В10.Мотоциклист и велосипедист одновременно начинают движение из состоянием покоя. Ускорение мотоциклиста в три раза больше, чем велосипедиста. Во сколько раз бóльшую скорость разовьет мотоциклист: а) за одно и то же время; б) на одном а том же пути?

В11.При скорости υ₁ = 15 км/ч тормозной путь автомоби­ля равен s = = 1,5 м. Каким будет тормозной путь s₂ при скорости υ₂ = 90 км/ч? Ускорение в обоих случаях одно и то же.

В12.Тело, имея начальную ско­рость υ₀ = 1 м/с, двигалось рав­ноускоренно и приобрело, пройдя некоторое расстояние, скорость υ_кон = = 7 м/с. Какова была скорость тела на половине этого расстоя­ния?

В13. Тело, двигаясь равноускоренно без начальной скорости, пройдя некоторый путь, достигло скорости υ₂ = 14 м/с. Чему была равна скорость υ₁ тела, когда оно прошло только k-ю часть этого пути? Разобрать случай, когда k = 2.

В14.Тормозной путь поезда перед остановкой на станции составляет 1000 м. Определить тормозное ускорение и тормозное время, если в начале торможения скорость поезда была 72 км/ч. Какова была скорость поезда у светофора, находящегося в средней точке тормозного пути?__

В15.При торможении от скорости υ₁ = 40 км/ч до полной остановки автомобиль прошёл путь s₁ = 16 м. Какой путь пройдёт этот автомобиль при снижении скорости от υ₂ = 100 км/ч до υ₃ = 60 км/ч? Считать, что величина ускорения в обоих случаях одинакова и постоянна.

Задачи трудные

С1.Тело, вышедшее из некоторой точки О, двигалось с постоянным по величине и направлению ускорением. Скорость его в конце 5-й секунды была 1,5 м/с, в конце 6-й секунды те­ло остановилось и затем стало двигаться обратно. Найти путь, пройден­ный телом до остановки. Определить скорость, с которой тело вернулось обратно в точку О.

С2.Двигаясь равноускоренно, тело проходит за про­межуток времени Dt₁ = 4с путь Ds₁= 2 м, а за сле­дующий промежуток времени Dt₂ = 5 с путь Ds₂ = 4 м. Определить ускорение тела и его начальную скорость.

С3.Водитель автомашины, нарушив правила движения, промчался по шоссе мимо поста ГАИ со скоростью υ₀ = 72 км/ч и продолжал далее ехать с такой же скоростью. Через время t₀ = 20 с вслед за нарушителем отправился на мотоцикле инспектор и, двигаясь равноускоренно, догнал нарушителя на расстоянии s = 12 км от поста. На какой скорости υ_x инспектор догнал нарушителя? Задачу решить графически.

C4.Пассажир первого вагона поезда длины l прогуливался по перрону. Когда он был рядом с последним вагоном, поезд начал двигаться с ускорением а. Пассажир сразу же побежал со скоростью υ. Через какое время он догонит свой вагон?

С5. Два автомобиля движутся навстречу друг другу один – с начальной скоростью υ₁ = 36 км/ч и ускорением а₁ = 0,30 м/с², а второй – с начальной ско­ростью υ₂ = 54 км/ч и ускорением а₂ = 0,50м/с². Начальное расстояние между ними L = 250 м. Через какое время встретятся автомобили и какое расстояние пройдёт каждый из них до встречи? Какую скорость будет иметь каждый из автомо­билей в момент встречи?

С6.Два мотоциклиста выезжают навстречу друг другу из пунктов А и В. Первый из пункта А равнозамедленно поднимается в гору с начальной скоростью υ₁ = 72 км/ч и с ускорением а = 2,0 м/с², второй – с начальной скоростью υ₂ = 36 км/ч равноускоренно спускается с горы из пунк­та В с таким же по величине ускорением.

Определить время движения и расстояние, пройденное первым мотоциклистом до встречи, если расстояние между пунктами А и В равно s = 300 м. Указать, как будет ме­няться со временем расстояние между мотоциклистами. По­строить график изменения расстояния между мотоцикли­стами с течением времени. Как определить по этому гра­фику момент встречи мотоциклистов?

С7.Из точки А выходит тело, движущееся с начальной скоростью υ₁ = 3 м/с и ускорением a₁ = 2 м/с². Спустя секунду из точки В выходит другое тело, движущееся навстречу первому с постоян­ной скоростью υ₂ = = 5 м/с. Расстояние АВ равно s = 100 м. Сколь­ко времени будет двигаться первое тело до встречи со вторым?

С8. Тело, трогаясь с места, за k-ю секунду равно­ускоренного движения проходит путь Ds_k. Рассчитать скорость тела в конце k-й секунды υ_k и путь, пройденный телом за k секунд s_k. Разобрать случай, когда k = 5, Ds_k = 45 м.

С9. За пятую секунду движения с постоянным ускорением тело проходит путь Ds₅ = 5,0 м и останавливается. Какой путь Ds₂ проходит это тело за вторую секунду этого движения?

Указание: задача имеет, по крайней мере, три способа решения.

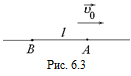С10. Тело начинает двигаться из точки А со скоростью υ₀ и через некоторое время попадает в точку В (рис. 6.3). Какой путь прошло тело, если оно двигалось равнопеременно с ускорением, численно равным а? Расстояние между точками А и В равно l. Найти среднюю скорость тела.

С11. На наклонную плоскость после начального толчка снизу вверх вкатывается шарик. На расстоянии l = 30 см от начала пути шарик побывал дважды: через t₁ = 1,0 c и t₂ = 2,0 с после начала движения. Считая движение равнопеременным, определите начальную ско­рость υ₀ и ускорение а.

С12.Мальчик бросил колесо, которое покатилось вверх по наклонной плоскости с начальной скоростью υ₀ и сразу же побежал за ним с постоянной скоростью и. Через какое время t мальчик поймал колесо, если оно двигалось с постоянным по модулю ускорением и через время t₀ повернуло в обратную сторону? Задачу решить графически.

С13.Тело двигалось по оси х с постоянным ускорением. В точке х₂ = 2 м оно имело скорость υ₂ = 2 м/с, а в точке х₃ = 3 м имело скорость υ₃ = 3 м/с. (Обе скорости направлены в положительную сторону оси х.) Было ли это тело в точке х₁ = 1 м?

С14.Доска, разделенная на пять равных отрезков, начинает скользить по наклонной плоскости. Первый отрезок прошел мимо отметки, сделанной на наклонной плоскости в том месте, где находился передний край доски в начале движения, за t = 2,0 с. За какое время пройдет мимо этой отметки послед­ний отрезок доски? Движение доски считать равноускорен­ным.

С15.Тело, трогаясь с места, движется равноускорен­но. Путь, проходимый телом, разбит на равные учас­тки Ds. Во сколько раз время Dt₁, затраченное на прохождение первого участка Ds₁, больше време­ни Dt_k, затраченного на прохождение k-го участка?