Соединении проводников

Пусть N проводников соединены параллельно (рис. 11.8). Пусть сила тока в неразветвленной части цепи равнаI₀, сила тока в 1-м проводнике равнаI₁, во вто­ром –I₂, в третьем – I₃ и т.д., в N-м – I_N.

Тогда справедливо соотношение:

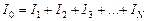. (11.4)

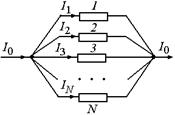Рис. 11.8

Читатель: А почему?

Автор: Давайте разберемся.

Пусть через поперечное сечение провод­ника в неразветвленной части цепи за некоторое время Dt проходит заряд Dq. Тогда: 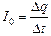, отсюда

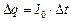. (1)

Пусть за это же время через поперечное сечение 1-го проводника проходит заряд Dq₁, через поперечное сечение 2-го проводника – заряд Dq₂, и т.д., через поперечное сечение N-го проводника – заряд Dq_N. Тогда справедливы соотношения:

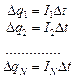(2)

Из закона сохранения заряда следует, что

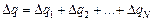. (3)

Ведь, в самом деле, исчезнуть заряд Dq не может, а двигаться из неразветвленной части он может только в разветвленную, т.е. через проводники 1, 2, ..., N. Больше просто некуда!

Подставляя выражения дляDq из (1), Dq₁, Dq₂, ..., Dq_Nиз (2), в (3) получим:

.

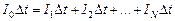ВынесемDt за скобку:

.

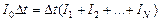Сокращая наDt, получим окончательное выражение:

,

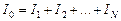что и требовалось доказать.

Равенство напряжений на проводниках,