Заземление проводников
Читатель: Что произойдет, если шар радиуса r, заряженный зарядом q, заземлить, т.е. соединить с поверхностью Земли? Например, соединив шар с трубой парового отопления.
Автор: Все будет происходить так, как если бы мы соединили наш проводник с огромным незаряженным шаром радиуса R >> r. После заземления потенциалы нашего шарика и огромного шара сравняются:
j = 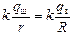 ,
,
где qш – заряд шарика, а qз – заряд Земли после заземления. Отсюда
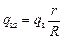 ,
,
если R ® ¥, а qз + qш = q, то очевидно, что qш ® 0. То есть весь заряд стечет на Землю.
СТОП! Решите самостоятельно: А1, А2.
Читатель: Как с помощью положительно заряженного тела зарядить незаряженный проводник отрицательно, не изменив заряда первого тела?
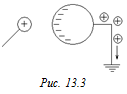 Автор: Поднесем к незаряженному заземленному проводнику заряженное тело (рис. 13.3). Из-за индукции на проводнике соберутся отрицательные заряды, а положительные уйдут «в Землю». Если убрать заземление, проводник останется отрицательно заряженным.
Автор: Поднесем к незаряженному заземленному проводнику заряженное тело (рис. 13.3). Из-за индукции на проводнике соберутся отрицательные заряды, а положительные уйдут «в Землю». Если убрать заземление, проводник останется отрицательно заряженным.
СТОП! Решите самостоятельно: А3, В1, В2, В6.
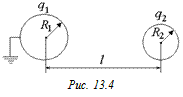 Задача 13.3. Два шара радиусами R1 и R2 и зарядами q1 и q2 находятся на расстоянии l друг от друга (рис. 13.3). Первый шар заземлили. Определить заряд на первом шаре после заземления.
Задача 13.3. Два шара радиусами R1 и R2 и зарядами q1 и q2 находятся на расстоянии l друг от друга (рис. 13.3). Первый шар заземлили. Определить заряд на первом шаре после заземления.
| q1 q2 R1 R2 l | Решение. После заземления потенциал первого шара стал равен потенциалу Земли, т.е. нулю.
Тогда
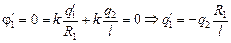 .
Ответ: .
Ответ: 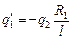 . .
|
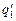 = ? = ?
|
СТОП! Решите самостоятельно: В4, С10, С11.
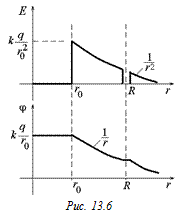
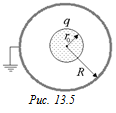 Задача 13.4. Внутри незаряженной проводящей сферы радиуса R находится металлический шарик радиуса r0 и заряда q (рис. 13.5). Сферу заземляют. Какой заряд Q будет на сфере? Нарисовать картину силовых линий до и после заземления. Построить графики Е(r) и j(r) до и после заземления.
Задача 13.4. Внутри незаряженной проводящей сферы радиуса R находится металлический шарик радиуса r0 и заряда q (рис. 13.5). Сферу заземляют. Какой заряд Q будет на сфере? Нарисовать картину силовых линий до и после заземления. Построить графики Е(r) и j(r) до и после заземления.
| R, r0, q | Решение. Графики Е(r) и j(r) до заземления представлены на рис. 13.6, картина силовых линий – на рис. 13.7. Мы уже обсуждали эти графики, поэтому повторяться не будем. Главное для нас сейчас – разобраться, что произойдет после заземления. |
| Q = ? Е(r) = ? j(r) = ? | |
 После заземления потенциал на поверхности сферы станет равным нулю, т.е. работа по перемещению заряда с поверхности сферы на бесконечность станет равной нулю. А это значит, что напряженность поля за поверхностью сферы будет равна нулю: Е(r) = 0 для r > l. Другими словами, за пределами сферы поле исчезнет!
После заземления потенциал на поверхности сферы станет равным нулю, т.е. работа по перемещению заряда с поверхности сферы на бесконечность станет равной нулю. А это значит, что напряженность поля за поверхностью сферы будет равна нулю: Е(r) = 0 для r > l. Другими словами, за пределами сферы поле исчезнет!
Рассмотрим поток вектора  через сферу S1 радиуса r > R (рис. 13.8):
через сферу S1 радиуса r > R (рис. 13.8):
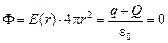 ,
,
где Q – искомый заряд сферы. Отсюда Q = –q.
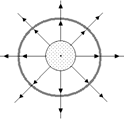
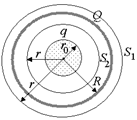
Рис. 13.7 Рис. 13.8
Теперь возьмем поток через сферу S2 радиуса r0 < r < R:
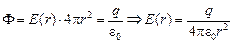 ,
,
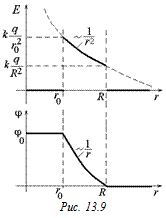 т.е. в этой области поле не изменилось.
т.е. в этой области поле не изменилось.
Графики Е(r) и j(r) после заземления представлены на рис. 13.9.
Потенциал в центре шара можно найти как сумму потенциалов полей, созданных зарядами на шаре и индуцированных зарядами на сфере:
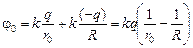 .
.
Ответ: Q = –q; рис. 13.7; графики на рис. 13.9.
СТОП! Решите самостоятельно: В7, С14.
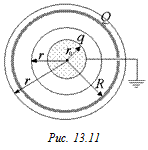
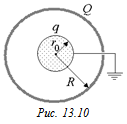 Задача 13.5. Внутри тонкой проводящей сферы радиуса R и с зарядом Q > 0 находится незаряженный проводящий шарик радиуса r0. Шарик заземляют проводом, проходящим через небольшое отверстие в сфере (рис. 13.10). Найти заряд q, который будет на шаре после заземления. Построить график Е(r), нарисовать картину силовых линий и определить потенциал сферы после заземления.
Задача 13.5. Внутри тонкой проводящей сферы радиуса R и с зарядом Q > 0 находится незаряженный проводящий шарик радиуса r0. Шарик заземляют проводом, проходящим через небольшое отверстие в сфере (рис. 13.10). Найти заряд q, который будет на шаре после заземления. Построить график Е(r), нарисовать картину силовых линий и определить потенциал сферы после заземления.
| Q, R, r0 | Решение. Читатель: Шарик первоначально не заряжен, Земля – тоже. Почему же при соединении |
| q = ? Е(r) = ? j(r) = ? |
двух незаряженных проводников между ними должно произойти какое-либо перераспределение заряда?
Автор: Потенциал поверхности незаряженного шара в начальный момент равен потенциалу поля, созданного зарядом сферы:
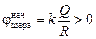 (если Q > 0).
(если Q > 0).
Потенциал же Земли 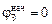 . Значит, положительные заряды будут перетекать от большего потенциала к меньшему. Следовательно, на шаре образуется отрицательный заряд.
. Значит, положительные заряды будут перетекать от большего потенциала к меньшему. Следовательно, на шаре образуется отрицательный заряд.
Читатель: А как же найти этот заряд?
 Автор: Потенциал поверхности шара после заземления, с одной стороны, равен нулю, а с другой – есть сумма потенциалов поля сферы и поля самого шара: jполя шара + jполя сферы = 0. Отсюда
Автор: Потенциал поверхности шара после заземления, с одной стороны, равен нулю, а с другой – есть сумма потенциалов поля сферы и поля самого шара: jполя шара + jполя сферы = 0. Отсюда 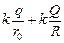 = 0, где q – искомый заряд шара. Тогда
= 0, где q – искомый заряд шара. Тогда
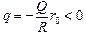 .
.
Построим график Е(r). Для этого вычислим поток через сферы радиусом r (рис. 13.11):
1) r0 < r < R, 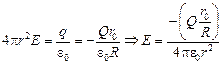 ;
;
2) r > R, 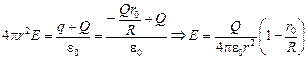 .
.
График Е(r) показан на рис. 13.12, а силовые линии – на рис. 13.13.
Потенциал сферы определим как алгебраическую сумму потенциалов полей шара и сферы:
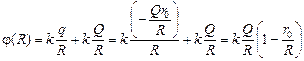 .
.
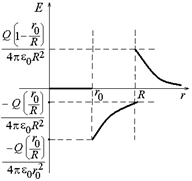
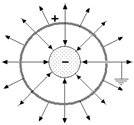
Рис. 13.12 Рис. 13.13
Ответ: 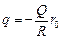 ;
; 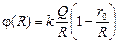 .
.
СТОП! Решите самостоятельно: В8, В9, С16, С18.
Дата добавления: 2016-04-11; просмотров: 8570;
